题目内容
1.已知ax+by=8,ax2+by2=22,ax3+by3=62,ax4+by4=178,试求1995(x+y)+6xy的值.分析 由(ax2+by2)(x+y)=(ax3+by3)+(ax+by)xy,(ax3+by3 )(x+y)=(ax4+by4)+(ax2+by2)(xy),把ax+by=8,ax2+by2=22,ax3+by3=62,ax4+by4=178代入可得关于(x+y),xy的方程组,由此求出x+y,xy即可解决问题.
解答 解:∵(ax2+by2)(x+y)=(ax3+by3)+(ax+by)xy,
(ax3+by3 )(x+y)=(ax4+by4)+(ax2+by2)(xy),
把ax+by=8,ax2+by2=22,ax3+by3=62,ax4+by4=178代入可得,
22(x+y)=62+8xy,62(x+y)=178+22xy,
解得x+y=5,xy=6,
∴1995(x+y)+6xy=1995×5+36=10011.
点评 本题考查因式分解的应用、多项式的乘法、方程组的解法等知识,解题的关键是灵活运用因式分解,构建方程组解决问题,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
10.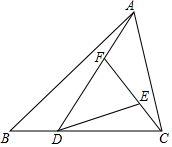 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{13}{18}$ | D. | $\frac{8}{27}$ |
7.与A(a,b)是反比例函数y=$\frac{k}{x}$上的一点,且a,b是关于x的一元二次方程x2-mx+5=0的两根,则反比例函数的解析式为( )
| A. | y=$\frac{1}{x}$ | B. | y=-$\frac{1}{x}$ | C. | y=$\frac{5}{x}$ | D. | y=-$\frac{5}{x}$ |
10.根据指令计算,完成如下填空:
a=-6,b=$\frac{1}{2}$,c=-2,d=-9,e=3,f=-$\frac{1}{4}$.
| 输入 | 执行操作 ×(-$\frac{1}{3}$) | 输出(入) | 执行操作 ÷(-12) | 输出(入) | 执行操作 ÷(-$\frac{1}{4}$) | 输出 |
| 18 | … | a | … | b | … | c |
| d | … | e | … | f | … | 1 |
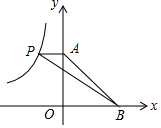 如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.
如图,反比例函数y=$\frac{k}{x}$的图象上有点P,PA⊥y轴于点A,点B在x轴的正半轴上,若△PAB的面积为6,则反比例函数的解析式是y=-$\frac{12}{x}$.
 根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是(a+b)(a-b)=a2-b2.
根据图①到图②的变化过程可以写出一个整式的乘法公式,这个公式是(a+b)(a-b)=a2-b2.