题目内容
7. 如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,AF=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,AF=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.(1)求证:四边形BDFC是平行四边形;
(2)若BF⊥CD,求四边形BDFC的面积.
分析 1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;
(2)由勾股定理列式求出AB,由平行四边形的面积公式列式计算即可得解.
解答 (1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
∵E是边CD的中点,
∴CE=DE,
在△BEC与△FED中,
$\left\{\begin{array}{l}{∠CBE=∠DFE}&{\;}\\{∠BEC=∠FED}&{\;}\\{CE=DE}&{\;}\end{array}\right.$,
∴△BEC≌△FED(AAS),
∴BE=FE,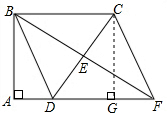
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)解:∵BF⊥CD,CE=DE,
∴BD=BC=AF-AD=20cm,
由勾股定理得,AB=$\sqrt{B{D}^{2}-A{D}^{2}}$=$\sqrt{2{0}^{2}-1{0}^{2}}$=10$\sqrt{3}$(cm),
∴四边形BDFC的面积=20×10$\sqrt{3}$=200$\sqrt{3}$(cm2).
点评 本题考查了平行四边形的判定,等腰三角形的性质,全等三角形的判定与性质,勾股定理;熟练掌握平行四边形的判定,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
19.在平行四边形ABCD中,∠A:∠B:∠C=2:1:2,则∠D=( )
| A. | 60° | B. | 72° | C. | 108° | D. | 120° |
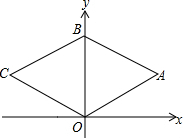 如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.
如图,菱形OABC顶点O是坐标原点,顶点B(0,6),OA=5.
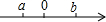 实数a、b在数轴上对应点的位置如图所示:则3a-$\sqrt{(a-b)^{2}}$=4a-b.
实数a、b在数轴上对应点的位置如图所示:则3a-$\sqrt{(a-b)^{2}}$=4a-b. 如图,E、F、G、H分别是?ABCD各边的中点.
如图,E、F、G、H分别是?ABCD各边的中点.