题目内容
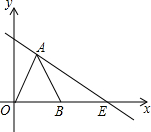 如图,△OAB是等边三角形,过点A的直线l:y=-
如图,△OAB是等边三角形,过点A的直线l:y=-
| ||
| 3 |
(1)求△OAB的边长;
(2)在直线l上是否存在点P,使得△PAB的面积是△OAB面积的一半?若存在,试求出点P的坐标;若不存在,请说明理由;
(3)过A、O、E三点画抛物线,将△OAB沿直线l方向平移到△O′A′B′,使得点B′在抛物线上,问平移的距离是多少?
考点:一次函数综合题
专题:综合题
分析:(1)将E坐标代入直线l解析式求出m的值,确定出直线l,根据三角形AOB为等边三角形,且A在直线l上,设等边三角形边长为2a,表示出A坐标,代入直线l方程求出a的值,即可确定出等边三角形边长;
(2)求出三角形AOB面积,由△PAB的面积是△OAB面积的一半,确定出三角形PAB面积,求出B到AE的距离BD,确定出AP长,由P在直线l上,设出P坐标为(p,-
p+
),利用两点间的距离公式求出p的值,确定出P坐标即可;
(3)求出过A,O,E三点抛物线解析式,找出过B且与l平行的直线方程,两者联立求出B′坐标,即可求出平移的距离.
(2)求出三角形AOB面积,由△PAB的面积是△OAB面积的一半,确定出三角形PAB面积,求出B到AE的距离BD,确定出AP长,由P在直线l上,设出P坐标为(p,-
| ||
| 3 |
4
| ||
| 3 |
(3)求出过A,O,E三点抛物线解析式,找出过B且与l平行的直线方程,两者联立求出B′坐标,即可求出平移的距离.
解答: 解:(1)将E(4,0)代入直线l方程得:0=-4×
解:(1)将E(4,0)代入直线l方程得:0=-4×
+m,即m=
,
∴直线l解析式为y=-
x+
,
过A作AC⊥OB,
∵△ABC为等边三角形,
∴OC=BC=
OB,
设等边△ABC边长为2a,则有OC=a,AC=
=
a,即A(a,
a),
代入直线l方程得:
a=-
a+
,
解得:a=1,即A(1,
),
则△ABC边长为2;
(2)过B作BD⊥AE,
∵直线l的斜率为-
,即倾斜角为150°,AB=BE=2,
∴∠AEB=∠BAE=30°,
∴BD=1,
∵S△PAB=
S△OAB,S△OAB=
×2×
=
,
∴S△PAB=
AP•BD=
AP=
,即AP=
,
设P坐标为(p,-
p+
),
∴AP2=(1-p)2+(
+
p-
)2=3,
解得:p=
或p=-
,
则P的坐标为(
,
)或(-
,
);
(3)设过A,E,O三点的抛物线解析式为y=ax2+bx,
将A(1,
),E(4,0)代入得:
,
解得:a=-
,b=
,
∴抛物线解析式为y=-
x2+
x,
由题意得:BB′∥l,过点B与l平行的直线解析式为y=-
(x-2),即y=-
x+
,
联立得:
,
解得:
或
,
∴平移的距离d=
=
|
=|
|,
则d=
或
.
 解:(1)将E(4,0)代入直线l方程得:0=-4×
解:(1)将E(4,0)代入直线l方程得:0=-4×
| ||
| 3 |
4
| ||
| 3 |
∴直线l解析式为y=-
| ||
| 3 |
4
| ||
| 3 |
过A作AC⊥OB,
∵△ABC为等边三角形,
∴OC=BC=
| 1 |
| 2 |
设等边△ABC边长为2a,则有OC=a,AC=
| OA2-OC2 |
| 3 |
| 3 |
代入直线l方程得:
| 3 |
| ||
| 3 |
4
| ||
| 3 |
解得:a=1,即A(1,
| 3 |
则△ABC边长为2;
(2)过B作BD⊥AE,
∵直线l的斜率为-
| ||
| 3 |
∴∠AEB=∠BAE=30°,
∴BD=1,
∵S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
设P坐标为(p,-
| ||
| 3 |
4
| ||
| 3 |
∴AP2=(1-p)2+(
| 3 |
| ||
| 3 |
4
| ||
| 3 |
解得:p=
| 5 |
| 2 |
| 1 |
| 2 |
则P的坐标为(
| 5 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
(3)设过A,E,O三点的抛物线解析式为y=ax2+bx,
将A(1,
| 3 |
|
解得:a=-
| ||
| 3 |
4
| ||
| 3 |
∴抛物线解析式为y=-
| ||
| 3 |
4
| ||
| 3 |
由题意得:BB′∥l,过点B与l平行的直线解析式为y=-
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
联立得:
|
解得:
|
|
∴平移的距离d=
| 2|xB′-xB| | ||
|
2
| ||
| 3 |
1±
| ||
| 2 |
| ||||
| 3 |
则d=
| ||||
| 3 |
| ||||
| 3 |
点评:此题属于一次函数综合题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,两点间的距离公式,两直线平行时斜率满足的关系,以及平移规律,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 如图,在△ABC中,DE∥BC,AD=2,AB=6,AE=3,则AC的长为
如图,在△ABC中,DE∥BC,AD=2,AB=6,AE=3,则AC的长为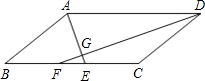 如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.
如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.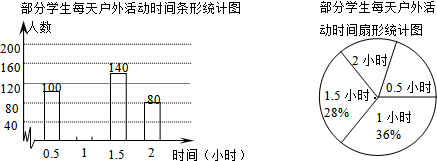
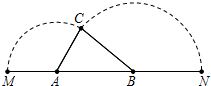 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x. 关于x的一元二次方程x2+(m+2)x+
关于x的一元二次方程x2+(m+2)x+