题目内容
已知一次函数的图象经过点A(2,3)和点B(-2,15)
(1)求AB的函数表达式;并画出图象.
(2)求图象与x轴、y轴的交点坐标C、D,并求出直线AB与坐标轴所围成的面积;
(3)如果点M(a,12)和N(4,b)在直线AB上,求a,b的值.
(1)求AB的函数表达式;并画出图象.
(2)求图象与x轴、y轴的交点坐标C、D,并求出直线AB与坐标轴所围成的面积;
(3)如果点M(a,12)和N(4,b)在直线AB上,求a,b的值.
考点:待定系数法求一次函数解析式,一次函数的图象,一次函数图象上点的坐标特征
专题:
分析:(1)利用待定系数法即可求得直线AB的解析式;
(2)在解析式中令x=0,即可求得与y轴的交点,令y=0,即可求得与x轴的交点,然后根据三角形的面积公式求解;
(3)把M、N的坐标分别代入函数解析式即可求得a、b的值.
(2)在解析式中令x=0,即可求得与y轴的交点,令y=0,即可求得与x轴的交点,然后根据三角形的面积公式求解;
(3)把M、N的坐标分别代入函数解析式即可求得a、b的值.
解答:解:(1)设直线AB的解析式是y=kx+b,
根据题意得:
,
解得:
,
则函数的解析式是y=-3x+9.
 ;
;
(2)y=-3x+9中,令x=0,解得:y=9,则D的坐标是(0,9);
令y=0,解得:x=3,则C的坐标是(3,0).
则直线AB与坐标轴所围成的面积是:
×3×9=
;
(3)(a,12)代入y=-3x+9,得-3a+9=12,解得:a=-1;
把(4,b)代入y=-3x+9得:-12+9=b,解得:b=-3.
根据题意得:
|
解得:
|
则函数的解析式是y=-3x+9.
 ;
;(2)y=-3x+9中,令x=0,解得:y=9,则D的坐标是(0,9);
令y=0,解得:x=3,则C的坐标是(3,0).
则直线AB与坐标轴所围成的面积是:
| 1 |
| 2 |
| 27 |
| 2 |
(3)(a,12)代入y=-3x+9,得-3a+9=12,解得:a=-1;
把(4,b)代入y=-3x+9得:-12+9=b,解得:b=-3.
点评:主要考查了用待定系数法求函数的解析式.先根据条件列出关于字母系数的方程,解方程求解即可得到函数解析式.当已知函数解析式时,求函数中字母的值就是求关于字母系数的方程的解.

练习册系列答案
相关题目
下列运算正确的是( )
| A、3a+2a=5a2 | ||
B、
| ||
| C、x2+x2=2x2 | ||
| D、x6÷x2=x3 |
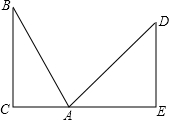 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点,当它靠在另一侧墙时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离DE=3
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点,当它靠在另一侧墙时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离DE=3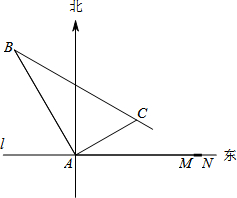 在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5
在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.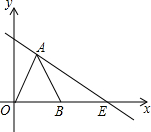 如图,△OAB是等边三角形,过点A的直线l:y=-
如图,△OAB是等边三角形,过点A的直线l:y=-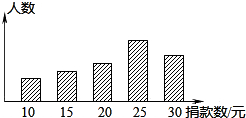 为支持我国西南地区抗旱救灾,团中央和全国少工委号召全国各级共青团和少先队组织,积极组织动员广大共青团员和少先队员,每人捐助一瓶水,用实际行动向灾区人民群众送去“爱心水”. 某校对本校倡导的自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人.请你根据上述信息解答下列问题:
为支持我国西南地区抗旱救灾,团中央和全国少工委号召全国各级共青团和少先队组织,积极组织动员广大共青团员和少先队员,每人捐助一瓶水,用实际行动向灾区人民群众送去“爱心水”. 某校对本校倡导的自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人.请你根据上述信息解答下列问题: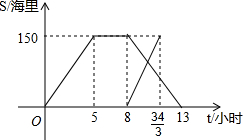 一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行).下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.