��Ŀ����
 ����x��һԪ���η���x2+��m+2��x+
����x��һԪ���η���x2+��m+2��x+| m-9 |
| 2 |
��1����֤������mȡ��ֵʱ������������������ȵ�ʵ������
��2����������y=x2+��m+2��x+
| m-9 |
| 2 |
��3���ڣ�2���������£��Ե�AΪֱ�Ƕ�����ֱ��������ACD��б��CD�������߽��ڵ�P����CP=DP����ֱ��AD��Ӧ�ĺ�������ʽ����P�����꣮
���㣺���κ����ۺ���
ר�⣺
��������1���õ�������б�ʽ����0���ɵõ�����������������ȵ�ʵ������
��2��������������x�ύ��A��-1-n��0����B��-2+n��0�����㣬�õ������ߵĶԳ���Ϊֱ��x=-
��Ȼ������-
=-
���������m=1���Ӷ�ȷ�������߶�Ӧ�ĺ�������ʽΪy=x2+3x-4��Ȼ��ȷ��A��B��������꼴�ɣ�
��3�����ȸ���A��-4��0����C��0��-4�����E��0��4����Ȼ�����ô���ϵ����ȷ��ֱ��AD�Ľ���ʽ��Ȼ�����Rt��CAD�У�PD=PC�õ�AP=
CD=CP����P��x��x2+3x-4�����Ӷ��õ���x+4��2+3��x2+3x-4��2=x2+��x2+3x-4+4��2�����x��ֵ������õ�P�����꣮
��2��������������x�ύ��A��-1-n��0����B��-2+n��0�����㣬�õ������ߵĶԳ���Ϊֱ��x=-
| 3 |
| 2 |
| m+2 |
| 2 |
| 3 |
| 2 |
��3�����ȸ���A��-4��0����C��0��-4�����E��0��4����Ȼ�����ô���ϵ����ȷ��ֱ��AD�Ľ���ʽ��Ȼ�����Rt��CAD�У�PD=PC�õ�AP=
| 1 |
| 2 |
�����1��֤�����߹���x��һԪ���η���x2+��m+2��x+
=0��
���=��m+2��2-4��
=m2+2m+22=��m+1��2+21��
�ߣ�m+1��2��0��
���=��m+1��2+21��
������mȡ��ֵʱ������������������ȵ�ʵ������
��2���⣺����������x�ύ��A��-1-n��0����B��-2+n��0�����㣬
�������ߵĶԳ���Ϊֱ��x=-
��
��-
=-
��
��m=1��
�������߶�Ӧ�ĺ�������ʽΪy=x2+3x-4��
��A��B���������ֱ�Ϊ��-4��0������1��0����
��3���⣺��A��-4��0����C��0��-4����
��AO=CO��
���CAB=45�㣮
�ߡ�CAD=90�㣬
���EAO=45�㣮
��AO=OE��
��E��0��4����

��ֱ��AD��Ӧ�ĺ�������ʽΪy=kx+b��k��0����
��A��-4��0����E��0��4�����룬��
��
���
��
��ֱ��AD��Ӧ�ĺ�������ʽΪy=x+4��
��Rt��CAD��PD=PC��
��AP=
CD=CP��
��P��x��x2+3x-4����
�ࣨx+4��2+3��x2+3x-4��2=x2+��x2+3x-4+4��2��
��������x2+2x-4=0��
���x=-1��
��
���P��������-1+
��-1-
����P��-1-
��-1-
����
| m-9 |
| 2 |
���=��m+2��2-4��
| (m-9) |
| 2 |
�ߣ�m+1��2��0��
���=��m+1��2+21��
������mȡ��ֵʱ������������������ȵ�ʵ������
��2���⣺����������x�ύ��A��-1-n��0����B��-2+n��0�����㣬
�������ߵĶԳ���Ϊֱ��x=-
| 3 |
| 2 |
��-
| m+2 |
| 2 |
| 3 |
| 2 |
��m=1��
�������߶�Ӧ�ĺ�������ʽΪy=x2+3x-4��
��A��B���������ֱ�Ϊ��-4��0������1��0����
��3���⣺��A��-4��0����C��0��-4����
��AO=CO��
���CAB=45�㣮
�ߡ�CAD=90�㣬
���EAO=45�㣮
��AO=OE��
��E��0��4����

��ֱ��AD��Ӧ�ĺ�������ʽΪy=kx+b��k��0����
��A��-4��0����E��0��4�����룬��
|
���
|
��ֱ��AD��Ӧ�ĺ�������ʽΪy=x+4��
��Rt��CAD��PD=PC��
��AP=
| 1 |
| 2 |
��P��x��x2+3x-4����
�ࣨx+4��2+3��x2+3x-4��2=x2+��x2+3x-4+4��2��
��������x2+2x-4=0��
���x=-1��
| 5 |
���P��������-1+
| 5 |
| 5 |
| 5 |
| 5 |
���������⿼���˶��κ������ۺ�֪ʶ���漰����һԪ���η��̵ĸ����б�ʽ������ϵ���������Ľ���ʽ��֪ʶ���ۺ��Խ�ǿ���ѶȽϴ�

��ϰ��ϵ�д�
 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
�����Ŀ
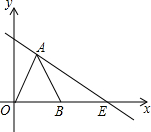 ��ͼ����OAB�ǵȱ������Σ�����A��ֱ��l��y=-
��ͼ����OAB�ǵȱ������Σ�����A��ֱ��l��y=-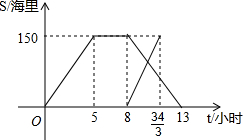 һ�죬ij�洬�뿪�ۿ�ǰ�����ҵ������㣬8Сʱ������ʱһ���������Ӹøۿڳ���ǰ�����ҵ�Ѳ�飨�������������洬��ͬһ���ߺ��У�����ͼ�����������洬���ۿڵľ���S���洬�뿪�ۿڵ�ʱ��t֮��ĺ���ͼ��
һ�죬ij�洬�뿪�ۿ�ǰ�����ҵ������㣬8Сʱ������ʱһ���������Ӹøۿڳ���ǰ�����ҵ�Ѳ�飨�������������洬��ͬһ���ߺ��У�����ͼ�����������洬���ۿڵľ���S���洬�뿪�ۿڵ�ʱ��t֮��ĺ���ͼ�� ��һ��Զ���У�С���ɼز��е��ҵغ�ԭ·���أ�С���ɼز��е��ҵغ�Ҳԭ·���أ���С���ڷ���;���ߵ�����ʱ������Ʒ�����������ҵأ����Ǵӱ������ҵأ�Ȼ����ԭ·���أ�����ͬʱ���������й����б������٣��貽�е�ʱ��Ϊt��h����������صľ���ֱ�ΪS1��km����S2��km����ͼ�е����߷ֱ��ʾS1��S2��t֮��ĺ�����ϵ��
��һ��Զ���У�С���ɼز��е��ҵغ�ԭ·���أ�С���ɼز��е��ҵغ�Ҳԭ·���أ���С���ڷ���;���ߵ�����ʱ������Ʒ�����������ҵأ����Ǵӱ������ҵأ�Ȼ����ԭ·���أ�����ͬʱ���������й����б������٣��貽�е�ʱ��Ϊt��h����������صľ���ֱ�ΪS1��km����S2��km����ͼ�е����߷ֱ��ʾS1��S2��t֮��ĺ�����ϵ��