题目内容
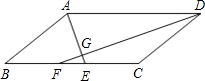 如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.
如图,在平行四边形ABCD中,∠BAD,∠ADC的平分线AE,DF分别与线段BC相交于点E,F,AE与DF相交于点G.(1)求证:AE⊥DF;
(2)若AD=10,AB=8,AG=4,求EC及EG的长.
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:(1)根据平行四边形的性质和平行线的性质得到∠BAD+∠ADC=180°;然后根据角平分线的性质推知∠DAE+∠ADF=
∠BAD+
∠ADC=90°,即∠AGD=90°.
(2)通过△AGD∽△EGF的对应边成比例来求EC及EG的长.
| 1 |
| 2 |
| 1 |
| 2 |
(2)通过△AGD∽△EGF的对应边成比例来求EC及EG的长.
解答:(1)证明:在平行四边形ABCD中,AB∥DC,
∴∠BAD+∠ADC=180°.
∵AE,DF分别是∠BAD,∠ADC的平分线,
∴∠DAE=∠BAE=
∠BAD,∠ADF=∠CDF=
∠ADC.
∴∠DAE+∠ADF=
∠BAD+
∠ADC=90°.
∴∠AGD=90°.
∴AE⊥DF.
(2)解:在平行四边形ABCD中,AD∥BC,BC=AD=10,
∴∠DAE=∠AEB,∠ADF=∠DFC.
由(1)得∠BAE=∠AEB,∠CDF=∠DFC.
∵AB=DC=8,
∴BE=AB=8,FC=CD=8.
∴EC=BC-BE=2.
∴EF=FC-EC=6.
∵AD∥BC,
∴∠DAG=∠FEG,∠ADG=∠EFG.
∴△AGD∽△EGF.
∴
=
.
∴
=
.
∴EG=
.
∴∠BAD+∠ADC=180°.
∵AE,DF分别是∠BAD,∠ADC的平分线,
∴∠DAE=∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DAE+∠ADF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AGD=90°.
∴AE⊥DF.
(2)解:在平行四边形ABCD中,AD∥BC,BC=AD=10,
∴∠DAE=∠AEB,∠ADF=∠DFC.
由(1)得∠BAE=∠AEB,∠CDF=∠DFC.
∵AB=DC=8,
∴BE=AB=8,FC=CD=8.
∴EC=BC-BE=2.
∴EF=FC-EC=6.
∵AD∥BC,
∴∠DAG=∠FEG,∠ADG=∠EFG.
∴△AGD∽△EGF.
∴
| AD |
| EF |
| AG |
| EG |
∴
| 10 |
| 6 |
| 4 |
| EG |
∴EG=
| 12 |
| 5 |
点评:本题考查了平行四边形的判定与性质、相似三角形的判定与性质.解题时,一定要数形结合,便于求得相关线段间的数量关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果关于x的一元二次方程x2+px+q=0的两根分别为x1=2,x2=-1,那么p,q的值分别是( )
| A、1,-2 | B、-1,-2 |
| C、-1.2 | D、1,2 |
下列运算正确的是( )
| A、3a+2a=5a2 | ||
B、
| ||
| C、x2+x2=2x2 | ||
| D、x6÷x2=x3 |
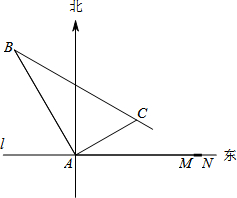 在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5
在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5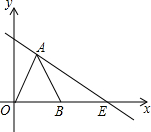 如图,△OAB是等边三角形,过点A的直线l:y=-
如图,△OAB是等边三角形,过点A的直线l:y=-