题目内容
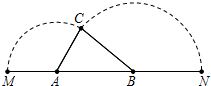 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.(1)求x的取值范围;
(2)若△ABC为等腰三角形,求x的值;
(3)探究:△ABC是否可能为直角三角形?若可能求出此时x的值,不可能请说明理由.
考点:旋转的性质
专题:计算题
分析:(1)由MB>1得3-x>1,解得x<2,再根据旋转的性质得AC=AM=1,BC=BN=3-x,根据三角形三边的关系得1+x>3-x,解得x>1,由此得到x的取值范围为1<x<2;
(2)由于1<x<2,则当AB=BC,即x=3-x,△ABC为等腰三角形时,于是得到x=
;
(3)由于1<x<2,AC不能为斜边,利用勾股定理分类讨论:当AC2+BC2=AB2,AB为斜边时,即12+(3-x)2=x2;当BC为斜边时,AC2+AB2=BC2,即12+x2=(3-x)2,然后分别解方程求出对应x的值.
(2)由于1<x<2,则当AB=BC,即x=3-x,△ABC为等腰三角形时,于是得到x=
| 2 |
| 3 |
(3)由于1<x<2,AC不能为斜边,利用勾股定理分类讨论:当AC2+BC2=AB2,AB为斜边时,即12+(3-x)2=x2;当BC为斜边时,AC2+AB2=BC2,即12+x2=(3-x)2,然后分别解方程求出对应x的值.
解答:解:(1)∵MN=4,MA=1,AB=x,
∴BN=4-1-x=3-x,
∵MB>1,
∴3-x>1,解得x<2,
∵以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,
∴AC=AM=1,BC=BN=3-x,
∵1+x>3-x,解得x>1,
∴x的取值范围为1<x<2;
(2)∵1<x<2;
∴△ABC为等腰三角形时,AB=BC,即x=3-x,
∴x=
;
(3)∵1<x<2,
∴AC不能为斜边,
当AC2+BC2=AB2,即AB为斜边时,
∴12+(3-x)2=x2,解得x=
;
当BC为斜边时,即AC2+AB2=BC2,
∴12+x2=(3-x)2,解得x=
,
∴当x=
或
时,△ABC为直角三角形.
∴BN=4-1-x=3-x,
∵MB>1,
∴3-x>1,解得x<2,
∵以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,
∴AC=AM=1,BC=BN=3-x,
∵1+x>3-x,解得x>1,
∴x的取值范围为1<x<2;
(2)∵1<x<2;
∴△ABC为等腰三角形时,AB=BC,即x=3-x,
∴x=
| 2 |
| 3 |
(3)∵1<x<2,
∴AC不能为斜边,
当AC2+BC2=AB2,即AB为斜边时,
∴12+(3-x)2=x2,解得x=
| 5 |
| 3 |
当BC为斜边时,即AC2+AB2=BC2,
∴12+x2=(3-x)2,解得x=
| 4 |
| 3 |
∴当x=
| 5 |
| 3 |
| 4 |
| 3 |
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了三角形三边的关系和勾股定理.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
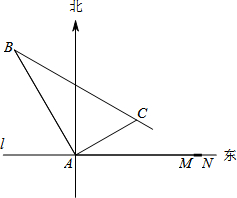 在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5
在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5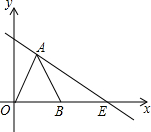 如图,△OAB是等边三角形,过点A的直线l:y=-
如图,△OAB是等边三角形,过点A的直线l:y=-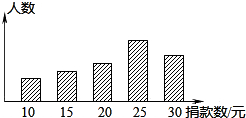 为支持我国西南地区抗旱救灾,团中央和全国少工委号召全国各级共青团和少先队组织,积极组织动员广大共青团员和少先队员,每人捐助一瓶水,用实际行动向灾区人民群众送去“爱心水”. 某校对本校倡导的自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人.请你根据上述信息解答下列问题:
为支持我国西南地区抗旱救灾,团中央和全国少工委号召全国各级共青团和少先队组织,积极组织动员广大共青团员和少先队员,每人捐助一瓶水,用实际行动向灾区人民群众送去“爱心水”. 某校对本校倡导的自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人.请你根据上述信息解答下列问题: