题目内容
4.解不等式:$\frac{2x+1}{3}-1<\frac{x-1}{2}$.分析 利用不等式的基本性质先去掉分母、去括号,再把不等号右边的x移到左边,合并同类项即可求得原不等式的解集.
解答 解:$\frac{2x+1}{3}-1<\frac{x-1}{2}$,
2(2x+1)-6<3(x-1),
4x+2-6<3x-3,
4x-3x<6-2-3,
x<1.
点评 本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
相关题目
14.若关于x、y的方程mx+ny=6的两个解是$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=6}\\{y=6}\end{array}\right.$,则( )
| A. | $\left\{\begin{array}{l}{m=-4}\\{n=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=4}\\{n=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=4}\\{n=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-4}\\{n=3}\end{array}\right.$ |
12.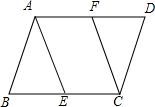 在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
 在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
在?ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )| A. | AF=CE | B. | AE=CF | C. | ∠BAE=∠FCD | D. | ∠BEA=∠FCE |
16.估计$\sqrt{5}$-1的结果在两个整数( )
| A. | 1与2之间 | B. | 2与3之间 | C. | 3与4之间 | D. | 0与1之间 |
14.若3x2a+by2与-4x3y3a-b是同类项,则a-b的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,直线a∥b,一块含有45°的直角三角尺如图放置,∠1=125°,则∠2=80°.
如图,直线a∥b,一块含有45°的直角三角尺如图放置,∠1=125°,则∠2=80°.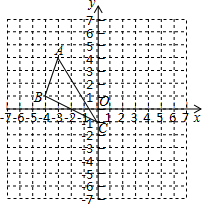 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-3,4),B(-4,1),C(0,-1).将△ABC向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′,其中点A′,B′,C′分别为点A,B,C的对应点.
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(-3,4),B(-4,1),C(0,-1).将△ABC向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′,其中点A′,B′,C′分别为点A,B,C的对应点.