题目内容
9.已知足球球门高是2.44米.足球教练使用仪器对某球员的一次射门进行了数据测试,球员在球门正前方8米处将球射向球门.在足球运行时,设足球运行的水平距离为x(米),足球与地面的高度为y(米).得到如下数据:| x(米) | … | 0 | 1.8 | 3 | 6 | 7.2 | 9 | … |
| y(米) | … | 0 | 1.53 | 2.25 | 3 | 2.88 | 2.25 | … |
(2)试通过计算,判断该运动员能否射球入门?
(3)假设该运动员每次射门时足球运动路线固定不变.
①点球时规定运动员在球门正前方11米处起脚将球射向球门,若该运动员参加点球射门,能否将球射门成功?
②若要保证射门成功,请直接写出该运动员在球门正前方的起脚位置离球门距离的范围.
分析 (1)利用描点法画出图象,可知函数是二次函数,利用待定系数法即可解决问题.
(2)求出x=8时的函数值y与2.44比较即可判断.
(3)①求出平移后的抛物线解析式,求出x=8时的函数值y与2.44比较即可判断.
②设抛物线向右平移a个单位得到,y=-$\frac{1}{12}$(x-6-a)2+3,当x=8时,y=2.44,2.44=-$\frac{1}{12}$(2-a)2+3,求出a的值即可解决问题,同样设抛物线向左平移a个单位得到y=-$\frac{1}{12}$(x-6+a)2+3,当x=8时,y=2.44,2.44=-$\frac{1}{12}$(2+a)2+3,求出a的值即可解决问题.
解答 解:(1)如图所示:猜想y是x的二次函数.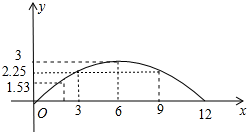
设y关于x的函数关系式为y=ax2+bx(a≠0),
由题意,选取(3,2.25),(6,3)代入得:
$\left\{{\begin{array}{l}{9a+3b=2.25}\\{36a+6b=3}\end{array}}\right.$,
解得:a=$-\frac{1}{12}$,b=1,
∴y=-$\frac{1}{12}$x2+x.
(2)当x=8时,y=$\frac{8}{3}$>2.44,所以球不能射入球门.
(3)①由题意可知,抛物线向左平移3米,得:y=-$\frac{1}{12}$(x-3)2+3,
当x=8时,y=$\frac{11}{12}$<2.44.所以球能射入球门.
②设抛物线向右平移a个单位得到,y=-$\frac{1}{12}$(x-6-a)2+3,
当x=8时,y=2.44,2.44=-$\frac{1}{12}$(2-a)2+3,
解得a=2+$\frac{2\sqrt{42}}{5}$或2-$\frac{2\sqrt{42}}{5}$(舍弃),
∴0≤x≤6-$\frac{2\sqrt{42}}{5}$,
设抛物线向左平移a个单位得到y=-$\frac{1}{12}$(x-6+a)2+3,
当x=8时,y=2.44,2.44=-$\frac{1}{12}$(2+a)2+3,
解得a=$\frac{2\sqrt{42}}{5}$-2或-$\frac{2\sqrt{42}}{5}$-2(舍弃),
∴6+$\frac{2\sqrt{42}}{5}$≤x≤12.
综上所述0≤x≤6-$\frac{2\sqrt{42}}{5}$或6+$\frac{2\sqrt{42}}{5}$≤x≤12.
点评 本题考查二次函数的应用、待定系数法等知识,解题的关键是学会构建二次函数解决实际问题,属于中考常考题型.

 观察函数y1=k1x+b1和y2=k2x+b2的图象,当x=1,两个函数值的大小为( )
观察函数y1=k1x+b1和y2=k2x+b2的图象,当x=1,两个函数值的大小为( )| A. | y1=y2 | B. | y1≥y2 | C. | y1>y2 | D. | y1<y2 |
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 一辆行驶中的汽车在某一分钟内速度的变化情况如图,下列说法正确的是( )
一辆行驶中的汽车在某一分钟内速度的变化情况如图,下列说法正确的是( )| A. | 在这一分钟内,汽车先提速,然后保持一定的速度行驶 | |
| B. | 在这一分钟内,汽车先提速,然后又减速,最后又不断提速 | |
| C. | 在这一分钟内,汽车经过了两次提速和两次减速 | |
| D. | 在这一分钟内,前40s速度不断化,后20s速度基本保持不变 |
 在Rt△ABC中,∠C=90°,CD是斜边AB上的高,∠ACD=55°,求∠B的度数.
在Rt△ABC中,∠C=90°,CD是斜边AB上的高,∠ACD=55°,求∠B的度数. 如图,已知在△ABC中,两条角平分线BE和CD相交于点F,若∠BFC=116°,求∠A的度数.
如图,已知在△ABC中,两条角平分线BE和CD相交于点F,若∠BFC=116°,求∠A的度数. 如图,一次函数的图象与正比例函数的图象交于点A,与两个坐标轴交于点B(-4,0),C(0,2)且S△AOB=2,求这两个函数的表达式.
如图,一次函数的图象与正比例函数的图象交于点A,与两个坐标轴交于点B(-4,0),C(0,2)且S△AOB=2,求这两个函数的表达式.