题目内容
12．
观察函数y1=k1x+b1和y2=k2x+b2的图象，当x=1，两个函数值的大小为（ ）| A． | y1=y2 | B． | y1≥y2 | C． | y1＞y2 | D． | y1＜y2 |
分析 在图中找到两函数图象的交点，根据图象即可作出判断．
解答 解：由图象可知当x=1时，y1＜y2．
故选：D．
点评 此题考查了直线交点坐标与一次函数组成的不等式组的解的关系，利用图象即可直接解答，体现了数形结合思想在解题中的应用．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
2．某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产为正、减产为负）：
（1）根据记录可知前三天共生产多少辆；
（2）产量最多的一天比产量最少的一天多生产多少辆；
（3）该厂实行每周计件工资制，每辆车60元，超额完成任务每辆奖15元，少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -2 | -4 | +13 | -10 | +16 | -9 |
（2）产量最多的一天比产量最少的一天多生产多少辆；
（3）该厂实行每周计件工资制，每辆车60元，超额完成任务每辆奖15元，少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？
3．二元一次方程组$\left\{\begin{array}{l}{x-y=4}\\{x+y=2}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=3}\\{y=-7}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=7}\\{y=3}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
20．下列各个运算中，结果为负数的是（ ）
| A． | -|-3| | B． | -（-3） | C． | （-3）2 | D． | （-2）×（-3） |
7．
为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：
（1）若某用户3月份用气量为60m3，交费多少元？
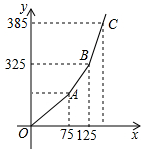
（2）调价后每月支付燃气费用y（单位：元）与每月用气量x（单位：m3）的关系如图所示，求y与x的解析式及a的值．
为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：| 每月用气量 | 单价（元/m3） |
| 不超出75m3的部分 | 2.5 |
| 超出75m3不超过125m3的部分 | a |
| 超出125m3的部分 | a+0.25 |
（2）调价后每月支付燃气费用y（单位：元）与每月用气量x（单位：m3）的关系如图所示，求y与x的解析式及a的值．
4．期中考试后，两位同学讨论他们所在小组的数学成绩，小明说：“我们组7位同学中，有4人的成绩是86分”，小亮说：“我们组7位同学中，第4名的成绩是86分”，上面两位同学所说的“86分”反映的统计量分别是（ ）
| A． | 众数和中位数 | B． | 众数与平均数 | C． | 众数和方差 | D． | 平均数与中位数 |
1．中招体育考试在即，为了解我校九年级学生的体育水平，随机抽取了九年级若干名学生的模拟测试成绩进行统计分析，并根据成绩分为四个等级（A、B、C、D），绘制了如下统计图表（不完整）：
请根据以上统计图表提供的信息，解答下列问题：
（1）本次抽查的学生有200名，成绩为B类的学生人数为100名，这组数据的中位数所在等级为B；
（2）请补全条形统计图；
（3）根据调查结果，请估计我校九年级学生（约900名）体育测试成绩为D类的学生人数．
| 成绩等级 | A | B | C | D |
| 人数 | 60 | 100 | 30 | 10 |
请根据以上统计图表提供的信息，解答下列问题：
（1）本次抽查的学生有200名，成绩为B类的学生人数为100名，这组数据的中位数所在等级为B；
（2）请补全条形统计图；
（3）根据调查结果，请估计我校九年级学生（约900名）体育测试成绩为D类的学生人数．
9．已知足球球门高是2.44米．足球教练使用仪器对某球员的一次射门进行了数据测试，球员在球门正前方8米处将球射向球门．在足球运行时，设足球运行的水平距离为x（米），足球与地面的高度为y（米）．得到如下数据：
（1）根据测试数据，在坐标系中描画草图，猜想y与x的函数关系，并求出函数关系式；
（2）试通过计算，判断该运动员能否射球入门？
（3）假设该运动员每次射门时足球运动路线固定不变．
①点球时规定运动员在球门正前方11米处起脚将球射向球门，若该运动员参加点球射门，能否将球射门成功？
②若要保证射门成功，请直接写出该运动员在球门正前方的起脚位置离球门距离的范围．
| x（米） | … | 0 | 1.8 | 3 | 6 | 7.2 | 9 | … |
| y（米） | … | 0 | 1.53 | 2.25 | 3 | 2.88 | 2.25 | … |
（2）试通过计算，判断该运动员能否射球入门？
（3）假设该运动员每次射门时足球运动路线固定不变．
①点球时规定运动员在球门正前方11米处起脚将球射向球门，若该运动员参加点球射门，能否将球射门成功？
②若要保证射门成功，请直接写出该运动员在球门正前方的起脚位置离球门距离的范围．