题目内容
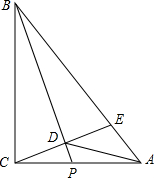 在Rt△ABC中,∠ACB=90°,AC=2,BC=4,P是线段AC上一个动点,连接BP,过C作CD⊥BP于D,交AB于E,连接AD,则下列关于线段AD的说法正确的是( )
在Rt△ABC中,∠ACB=90°,AC=2,BC=4,P是线段AC上一个动点,连接BP,过C作CD⊥BP于D,交AB于E,连接AD,则下列关于线段AD的说法正确的是( )A、存在最大值,最大值为
| ||||
B、存在最小值,最小值为2
| ||||
C、存在最小值,最小值为1-
| ||||
| D、存在最大值,但不存在最小值 |
考点:圆的综合题
专题:综合题
分析:根据垂线的定义得到∠CDB=90°,根据圆周角定理的推理得点D总在以BC为直径的圆上,所以当点D为OA与圆的交点时,线段AD最短,如图,再根据勾股定理计算出OA,然后利用AD=OA-OD计算即可.
解答: 解:∵CD⊥BP,
解:∵CD⊥BP,
∴∠CDB=90°,
∴点D总在以BC为直径的圆上,
∵线段AD的长为点A到圆上点D的距离,
∴当点D为OA与圆的交点时,线段AD最短,如图,
∵∠ACB=90°,AC=2,BC=4,
∴OC=2,
∴OA=
=2
,
∴AD=OA-OD=2
-2,
即线段AD存在最小值,最小值为2
-2.
故选B.
 解:∵CD⊥BP,
解:∵CD⊥BP,∴∠CDB=90°,
∴点D总在以BC为直径的圆上,
∵线段AD的长为点A到圆上点D的距离,
∴当点D为OA与圆的交点时,线段AD最短,如图,
∵∠ACB=90°,AC=2,BC=4,
∴OC=2,
∴OA=
| OC2+CA2 |
| 2 |
∴AD=OA-OD=2
| 2 |
即线段AD存在最小值,最小值为2
| 2 |
故选B.
点评:本题考查了圆的综合题:熟练掌握圆周角定理和圆外一点到圆上的最大或最小距离;会利用勾股定理计算线段的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列式子一定成立的是( )
| A、3x2-x2=3 |
| B、3a2+2a3=5a5 |
| C、3+x=3x |
| D、-6ab+6ab=0 |
方程x2-4x-6=0的根的情况是( )
| A、有两个相等实根 |
| B、有两个不等实根 |
| C、没有实根 |
| D、以上答案都有可能 |
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④BD=
| 3 |
其中正确的结论的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列结论错误的是( )
| A、若a=b,则a-c=b-c | ||||
| B、若ax=bx,则a=b | ||||
C、若a=b,则
| ||||
| D、若x=2,则x2=2x |
已知实数ab满足(a2+b2-1)(a2+b2+3)=12,那么( )
| A、a2+b2=3 |
| B、a2+b2=-5 |
| C、a2+b2=3或a2+b2=5 |
| D、a2+b2=2 |
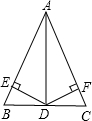 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有( )
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有( )