题目内容
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④BD=
| 3 |
其中正确的结论的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:正方形的性质,全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据三角形的全等的知识可以判断①的正误;
根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;
根据线段垂直平分线的知识可以判断③的正误;
利用解三角形求正方形的面积等知识可以判断④的正误.
根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;
根据线段垂直平分线的知识可以判断③的正误;
利用解三角形求正方形的面积等知识可以判断④的正误.
解答:解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=
,
设正方形的边长为a,
在Rt△ADF中,
AD2+DF2=AF2,即a2+(a-
)2=4,
解得a=
,
则a2=2+
,
S正方形ABCD=2+
,
④说法正确.
故选:C.
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
|
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,

∴AC⊥EF,且AC平分EF,
∵∠CAF≠∠DAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=
| 2 |
设正方形的边长为a,
在Rt△ADF中,
AD2+DF2=AF2,即a2+(a-
| 2 |
解得a=
| ||||
| 2 |
则a2=2+
| 3 |
S正方形ABCD=2+
| 3 |
④说法正确.
故选:C.
点评:本题主要考查正方形的性质的知识点,解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,此题难度不大,但是有一点麻烦.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 如图,在△ABC中,点E、F分别为AB、AC的中点.若EF的长为2,则BC的长为( )
如图,在△ABC中,点E、F分别为AB、AC的中点.若EF的长为2,则BC的长为( )| A、1 | B、2 | C、4 | D、8 |
如果(x+1)(x2-5ax+a)的乘积中不含x2项,则a为( )
| A、5 | ||
B、
| ||
C、-
| ||
| D、-5 |
下列调查适合普查的是( )
| A、夏季冷饮市场上冰淇淋的质量 |
| B、某本书中某页的印刷错误 |
| C、公民保护环境的意识 |
| D、某批灯泡的使用寿命 |
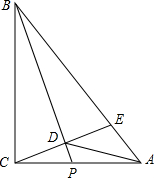 在Rt△ABC中,∠ACB=90°,AC=2,BC=4,P是线段AC上一个动点,连接BP,过C作CD⊥BP于D,交AB于E,连接AD,则下列关于线段AD的说法正确的是( )
在Rt△ABC中,∠ACB=90°,AC=2,BC=4,P是线段AC上一个动点,连接BP,过C作CD⊥BP于D,交AB于E,连接AD,则下列关于线段AD的说法正确的是( )A、存在最大值,最大值为
| ||||
B、存在最小值,最小值为2
| ||||
C、存在最小值,最小值为1-
| ||||
| D、存在最大值,但不存在最小值 |
下列方程中,解为x=1的是( )
| A、1-x=2 |
| B、2x-1=4-3x |
| C、3-(x-1)=4 |
| D、x-4=5x-2 |
下列因式分解正确的是( )
| A、x2+y2=(x+y)(x+y) |
| B、x2-y2=(x+y)(x-y) |
| C、-x2+y2=(-x+y)(-x-y) |
| D、-x2-y2=-(x+y)(x-y) |
 如图,在正方形网格中,△ABC的顶点都在格点上,则cos∠ABC的值为
如图,在正方形网格中,△ABC的顶点都在格点上,则cos∠ABC的值为 如图,AB为半圆O的直径,以AO为直径作半圆M,C为OB的中点,过点C作半圆M的切线交半圆M于点D,延长AD交圆O于点E,若AB等于4,求图中阴影部分的面积.
如图,AB为半圆O的直径,以AO为直径作半圆M,C为OB的中点,过点C作半圆M的切线交半圆M于点D,延长AD交圆O于点E,若AB等于4,求图中阴影部分的面积.