题目内容
已知实数ab满足(a2+b2-1)(a2+b2+3)=12,那么( )
| A、a2+b2=3 |
| B、a2+b2=-5 |
| C、a2+b2=3或a2+b2=5 |
| D、a2+b2=2 |
考点:换元法解一元二次方程
专题:
分析:设a2+b2=y,则原方程转化为关于y的一元二次方程,通过解方程可以求得y的值,即a2+b2的值.
解答:解:设a2+b2=y,则原方程转化为(y-1)(y+3)=12,
整理,得
(y+5)(y-3)=0,
解得 y1=-5(不合题意,舍去),y2=3.
则a2+b2=3.
故选:A.
整理,得
(y+5)(y-3)=0,
解得 y1=-5(不合题意,舍去),y2=3.
则a2+b2=3.
故选:A.
点评:本题主要考查了换元法,即把某个式子看作一个整体,用一个字母去代替它,实行等量替换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果(x+1)(x2-5ax+a)的乘积中不含x2项,则a为( )
| A、5 | ||
B、
| ||
C、-
| ||
| D、-5 |
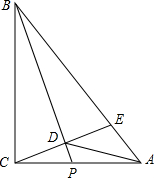 在Rt△ABC中,∠ACB=90°,AC=2,BC=4,P是线段AC上一个动点,连接BP,过C作CD⊥BP于D,交AB于E,连接AD,则下列关于线段AD的说法正确的是( )
在Rt△ABC中,∠ACB=90°,AC=2,BC=4,P是线段AC上一个动点,连接BP,过C作CD⊥BP于D,交AB于E,连接AD,则下列关于线段AD的说法正确的是( )A、存在最大值,最大值为
| ||||
B、存在最小值,最小值为2
| ||||
C、存在最小值,最小值为1-
| ||||
| D、存在最大值,但不存在最小值 |
下列方程中,解为x=1的是( )
| A、1-x=2 |
| B、2x-1=4-3x |
| C、3-(x-1)=4 |
| D、x-4=5x-2 |
 如图,修建抽水站时,沿着坡度为i=1:
如图,修建抽水站时,沿着坡度为i=1:| 3 |
| A、8m | B、10m |
| C、12m | D、18m |
下列因式分解正确的是( )
| A、x2+y2=(x+y)(x+y) |
| B、x2-y2=(x+y)(x-y) |
| C、-x2+y2=(-x+y)(-x-y) |
| D、-x2-y2=-(x+y)(x-y) |
关于x的一元二次方程x2+px-6=0的一个根为2,则p的值为( )
| A、-2 | B、2 | C、-1 | D、1 |