题目内容
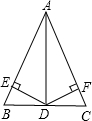 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有( )
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有( )| A、4个 | B、3个 | C、2个 | D、1个 |
考点:全等三角形的判定与性质,角平分线的性质,等腰三角形的性质
专题:计算题
分析:由AD为角平分线,DE垂直于AB,DF垂直于AC,利用角平分线定理得到DE=DF,根据AB=AC,利用三线合一得到D为BC的中点,AD垂直于BC,利用HL得到三角形ADE与三角形ADF全等,利用全等三角形对应边相等得到AE=AF,进而再利用HL得到三角形BDE与三角形CDF全等,利用SAS得到三角形ADB与三角形ADC全等,即可得到结果.
解答: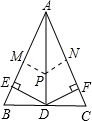 解:∵AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
解:∵AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,D为BC中点,AD⊥BC,
在Rt△ADE和Rt△ADF中,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠ADE=∠ADF,
∴DA平分∠EDF,
取AD上任意点P,作PM⊥AB,PN⊥AC,
∵AD平分∠BAC,
∴PM=PN;
在Rt△EBD和Rt△FCD中,
,
∴Rt△EBD≌Rt△FCD(HL);
在△ADB和△ADC中,
,
∴△ADB≌△ADC(SAS),即图形中全等三角形有3对,
则其中正确的个数有4个.
故选A.
 解:∵AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
解:∵AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,∴DE=DF,D为BC中点,AD⊥BC,
在Rt△ADE和Rt△ADF中,
|
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠ADE=∠ADF,
∴DA平分∠EDF,
取AD上任意点P,作PM⊥AB,PN⊥AC,
∵AD平分∠BAC,
∴PM=PN;
在Rt△EBD和Rt△FCD中,
|
∴Rt△EBD≌Rt△FCD(HL);
在△ADB和△ADC中,
|
∴△ADB≌△ADC(SAS),即图形中全等三角形有3对,
则其中正确的个数有4个.
故选A.
点评:此题考查了全等三角形的判定与性质,等腰三角形的性质,以及角平分线定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
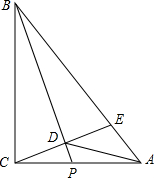 在Rt△ABC中,∠ACB=90°,AC=2,BC=4,P是线段AC上一个动点,连接BP,过C作CD⊥BP于D,交AB于E,连接AD,则下列关于线段AD的说法正确的是( )
在Rt△ABC中,∠ACB=90°,AC=2,BC=4,P是线段AC上一个动点,连接BP,过C作CD⊥BP于D,交AB于E,连接AD,则下列关于线段AD的说法正确的是( )A、存在最大值,最大值为
| ||||
B、存在最小值,最小值为2
| ||||
C、存在最小值,最小值为1-
| ||||
| D、存在最大值,但不存在最小值 |
 如图,修建抽水站时,沿着坡度为i=1:
如图,修建抽水站时,沿着坡度为i=1:| 3 |
| A、8m | B、10m |
| C、12m | D、18m |
下列因式分解正确的是( )
| A、x2+y2=(x+y)(x+y) |
| B、x2-y2=(x+y)(x-y) |
| C、-x2+y2=(-x+y)(-x-y) |
| D、-x2-y2=-(x+y)(x-y) |
已知一次函数y=kx+b的图象经过第一、二、四象限,则kb的值可以是( )
| A、-1 | B、0 | C、2 | D、任意实数 |
关于x的一元二次方程x2+px-6=0的一个根为2,则p的值为( )
| A、-2 | B、2 | C、-1 | D、1 |
 如图,在△ABC中,己知∠ACB=90°,CD⊥AB于D.若AD=8,BD=2,则AC=
如图,在△ABC中,己知∠ACB=90°,CD⊥AB于D.若AD=8,BD=2,则AC=