题目内容
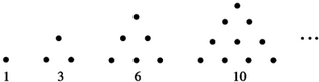
9.图中的三角形称为希尔宾斯三角形,在下面给出的四个三角形中,黑色的三角形个数依次构成一个数列的前四项,即a1,a2,a3,a4,依此着色方案继续对三角形着色,则第2015个黑色三角形的个数a2015=32014.
分析 结合图形发现规律“从第二个图形开始,每个图形中黑色三角形的个数都是前一个图形的3倍”,结合a1=1即可得出a2015的值,从而得出结论.
解答 解:观察图形发现:从第二个图形开始,每个图形中黑色三角形的个数都是前一个图形的3倍,
∴有a1=1,a2=3,a3=9,a4=27,…,${a}_{n}={3}^{(n-1)}$.
令n=2015可得:a2015=3(2015-1)=32014.
故答案为:32014.
点评 本题考查了图形的变化类,解题的关键是找出“从第二个图形开始,每个图形中黑色三角形的个数都是前一个图形的3倍”这一规律.本题属于基础题,难度不大,解决该题型题目时,根据图形的变化找出变化规律是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若关于x的不等式组$\left\{\begin{array}{l}{x-m<0}\\{7-2x≤1}\end{array}\right.$的整数解共有4个,则关于x的一元二次方程8x2-8x+m=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 有一个实数根 |
19.函数y=(m2-m)${x}^{{m}^{2}-3m+1}$是反比例函数,则( )
| A. | m≠0 | B. | m≠0且m≠1 | C. | m=2 | D. | m=1或2 |

 如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.
如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数50°.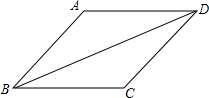 如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.
如图,菱形ABCD的边长为5,sin∠ABC=$\frac{4}{5}$,则对角线BD的长为4$\sqrt{5}$.