题目内容
13.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,A2在x轴上,依次进行下去….若点A(5,0),B(0,12),则点B2014的坐标为(12084,12).
分析 首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…每偶数之间的B相差30个单位长度,根据这个规律可以求得B2014的坐标.
解答 解:∵AO=5,BO=12,
∴AB=13,
∴OA+AB1+B1C2=5+13+12=30,
∴B2的横坐标为:30,且B2C2=12,
∴B4的横坐标为:2×30=60,
∴点B2014的横坐标为:1007×12=12084.
∴点B2014的纵坐标为:12.
故答案为:(12084,12).
点评 此题考查了点的坐标规律变换,通过图形旋转,找到所有B点之间的关系是本题的关键.题目难易程度适中,可以考察学生观察、发现问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成了一个四边形ABCD,试证明四边形ABCD是菱形.
如图,用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成了一个四边形ABCD,试证明四边形ABCD是菱形.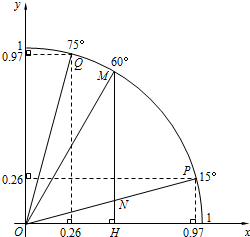 如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:
如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题: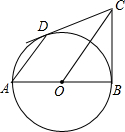 如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.
如图,已知AB为⊙O的直径,CB、CD分别切⊙O于点B、D.求证:AD∥OC.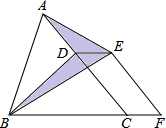 如图,已知△ABC的面积为36,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为36,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )