题目内容
4.古希腊数学家毕达哥拉斯把“数”当作“形”来研究,他称下面一些数为“三角形数”(如图),第1个“三角形数”是1,第2个是3,第3个是6,第4个是10,按照这个规律,第50个“三角形数”是1275.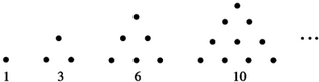
分析 研究图形发现规律“第n个“三角形数”是1+2+…+n=$\frac{n(n+1)}{2}$”,代入n=50即可得出结论.
解答 解:观察图形,发现第1个“三角形数”是1,第2个是1+2=3,第3个是1+2+3=6,第4个是1+2+3+4=10,…
由此发现规律:第n个“三角形数”是1+2+…+n=$\frac{n(n+1)}{2}$.
第50个“三角形数”是1+2+…+49+50=$\frac{50×(50+1)}{2}$=1275.
故答案为:1275.
点评 本题考查了图形的变化规律,解题关键是找出“第n个“三角形数”是1+2+…+n=$\frac{n(n+1)}{2}$”这一规律.本题属于基础题,难度不大,解决该题型题目时,分析图形得出规律是关键.

练习册系列答案
相关题目
8.关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=4k}\\{x-y=8k}\end{array}\right.$的解也是二元一次方程2x+3y=6的解,则k的值是( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
15.下列函数是二次函数的是( )
| A. | y=8x2+1 | B. | y=2x-3 | C. | y=3x2+$\frac{1}{{x}^{2}}$ |
16.n个连续偶数按规律排成表:
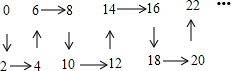
根据规律,从2016到2018,箭头的方向依次应为( )
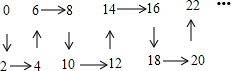
根据规律,从2016到2018,箭头的方向依次应为( )
| A. | ↑→ | B. | →↑ | C. | ↓→ | D. | →↓ |
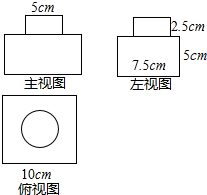 如图是一个铁制零件的三视图及尺寸标注.
如图是一个铁制零件的三视图及尺寸标注.