题目内容
1．
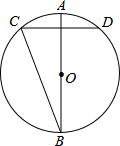如图，⊙O的直径AB垂直于弦CD，垂足为E．已知AB=10cm，CD=6cm．求CB的长．
分析 连接AC，由垂径定理可得AB平分CD，设AE=x，则BE=10-x，由射影定理可得CE2=AE•BE，易得x，在Rt△BCE中，由勾股定理易得CB的长．
解答 解：如图，
连接AC，
∵⊙O的直径AB垂直于弦CD，CD=6cm，
∴CE=DE=$\frac{1}{2}CD$=3cm，
设AE=x，则BE=10-x，
∴CE2=AE•BE，
即9=x（10-x），
解得：x1=9，x2=1，
∴AE=1，BE=9，
在Rt△BCE中，
CB=$\sqrt{{CE}^{2}{+BE}^{2}}$=$\sqrt{{3}^{2}{+9}^{2}}$=3$\sqrt{10}$．
点评 本题主要考查了垂径定理，作出辅助线，利用方程思想解得BE的长是解答此题的关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
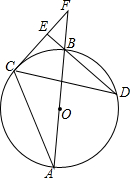AB为⊙O的直径，C，D为⊙O上不同于A，B的两点，∠ABD=2∠BAC，连接CD，过点C作CE⊥DB，垂足为E，直径AB与CE的延长线相交于F点．
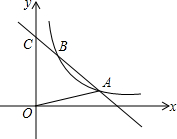如图，一次函数的图象与y轴交于C（0，4），且与反比例函数y=$\frac{k}{x}$（x＞0）的图象在第一象限内交于A（3，a），B（1，b）两点，