题目内容
12.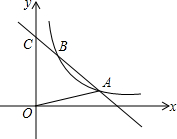 如图,一次函数的图象与y轴交于C(0,4),且与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限内交于A(3,a),B(1,b)两点,
如图,一次函数的图象与y轴交于C(0,4),且与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限内交于A(3,a),B(1,b)两点,(1)求△AOC的面积;
(2)若$\sqrt{{a}^{2}-2ab+{b}^{2}}$=2,求反比例函数和一次函数的解析式.
分析 (1)作AD⊥y轴于D,根据题意得出AD=3,OC=4,然后关键数据线面积公式即可求得;
(2)根据反比例函数系数k=xy,得出3a=b,然后代入$\sqrt{{a}^{2}-2ab+{b}^{2}}$=2,即可求得a的值,求得A的坐标,从而求得k的值,然后关键待定系数即可求得一次函数的解析式.
解答  解:(1)作AD⊥y轴于D,
解:(1)作AD⊥y轴于D,
∵A(3,a),
∴AD=3,
∵一次函数的图象与y轴交于C(0,4),
∴OC=4,
∴S△AOC=$\frac{1}{2}$OC•AD=$\frac{1}{2}$×4×3=6;
(2)∵A(3,a),B(1,b)两点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴3a=b,
∵$\sqrt{{a}^{2}-2ab+{b}^{2}}$=2,
∴a2-2ab+b2=4,
∴a2-2a•3a+(3a)2=4,
整理得,a2=1,
∵a>0,
∴a=1,
∴A(3,1),
∴k=3×1=3,
设直线的解析式为y=mx+n,
∴$\left\{\begin{array}{l}{n=4}\\{3m+n=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=4}\end{array}\right.$,
∴反比例函数和一次函数的解析式分别为y=$\frac{3}{x}$和y=-x+4.
点评 本题考查了反比例函数和一次函数的交点问题,三角形的面积,根据题意得出3a=b是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
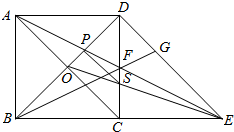
7. 如图所示,同时能用三个字母和一个字母表示的角是( )
如图所示,同时能用三个字母和一个字母表示的角是( )
 如图所示,同时能用三个字母和一个字母表示的角是( )
如图所示,同时能用三个字母和一个字母表示的角是( )| A. | ∠1 | B. | ∠2 | C. | ∠A和∠D | D. | ∠A和∠C |
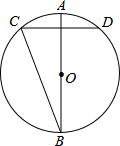 如图,⊙O的直径AB垂直于弦CD,垂足为E.已知AB=10cm,CD=6cm.求CB的长.
如图,⊙O的直径AB垂直于弦CD,垂足为E.已知AB=10cm,CD=6cm.求CB的长.