题目内容
13.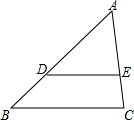 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
分析 根据DE∥BC,即可证得△ABC∽△ADE,然后利用相似三角形的面积的比等于相似比,即可证得两个三角形的面积的比,根据比例的性质即可求解.
解答 解:∵AD:DB=2:1,
∴$\frac{AD}{AB}=\frac{2}{3}$.
∵DE∥BC,
∴△ABC∽△ADE.
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}=\frac{4}{9}$.
∴$\frac{{S}_{△ADE}}{{S}_{四边形DBCE}}=\frac{4}{5}$.
故选C.
点评 本题考查了相似三角形的判断与性质,熟练运用相似三角形的性质是关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
15.用反证法证明“若a⊥c,b⊥c,则a∥b”时,应假设( )
| A. | a不垂直于c | B. | a,b都不垂直于c | C. | a与b相交 | D. | a⊥b |
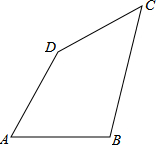 如图,四边形ABCD中,AB=AD=6cm,∠A=60°,BC=3$\sqrt{5}$cm,CD=3cm,求四边形ABCD的面积.
如图,四边形ABCD中,AB=AD=6cm,∠A=60°,BC=3$\sqrt{5}$cm,CD=3cm,求四边形ABCD的面积.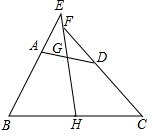 如图,四边形ABCD中,G,H分别是AD,BC的中点,AB=CD,BA,CD的延长线交HG的延长线于点E,F,求证:∠BEH=∠CFH.
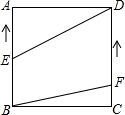
如图,四边形ABCD中,G,H分别是AD,BC的中点,AB=CD,BA,CD的延长线交HG的延长线于点E,F,求证:∠BEH=∠CFH.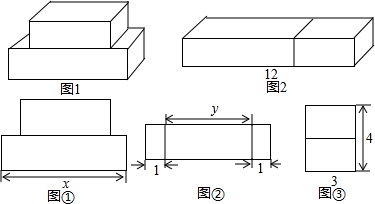
 如图,正方形ABCD的边长为6cm,动点E由B向A以2cm/s的速度移动,动点F由C向D以1cm/s的速度移动,E,F分别由B,C同时出发,问几秒钟后四边形BFDE是平行四边形?
如图,正方形ABCD的边长为6cm,动点E由B向A以2cm/s的速度移动,动点F由C向D以1cm/s的速度移动,E,F分别由B,C同时出发,问几秒钟后四边形BFDE是平行四边形? 如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.
如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.