题目内容
8.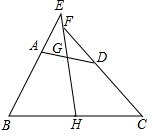 如图,四边形ABCD中,G,H分别是AD,BC的中点,AB=CD,BA,CD的延长线交HG的延长线于点E,F,求证:∠BEH=∠CFH.
如图,四边形ABCD中,G,H分别是AD,BC的中点,AB=CD,BA,CD的延长线交HG的延长线于点E,F,求证:∠BEH=∠CFH.
分析 如图,连接BD,作BD的中点M,连接HM、GM.利用三角形中位线定理证得△HMG是等腰三角形,则∠MHG=∠MGH.利用三角形中位线定理、平行线的性质推知∠MHG=∠AEH,∠MHG=∠DFH.根据等量代换证得∠BEH=∠CFH.
解答 证明:如图,连接BD,作BD的中点M,连接HM、GM.
∵点G是AD的中点,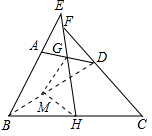
∴在△ABD中,GM∥AB,GM=$\frac{1}{2}$AB,
∴∠MHG=∠AEH,
同理可证:HM∥CD,HM=$\frac{1}{2}$CD.
∴∠MHG=∠DFH.
又∵AB=CD,∴GM=HM,
∴∠MHG=∠MGH 即∠BEH=∠CFH.
点评 此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半,题目的综合性较强,难度较大,解题的关键是正确添加辅助线.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
13.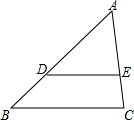 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
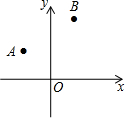 如图,在平面直角坐标系中,点A、B的坐标分别为(-1,2)、(1,4),欲在x轴上找一点P,使PA+PB最短,则点P的坐标为(-$\frac{1}{3}$,0).
如图,在平面直角坐标系中,点A、B的坐标分别为(-1,2)、(1,4),欲在x轴上找一点P,使PA+PB最短,则点P的坐标为(-$\frac{1}{3}$,0).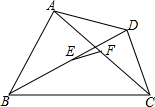 如图,在四边形ABCD中,AB>CD,E,F分别是对角线BD,AC的中点,求证:$\frac{1}{2}$(AB+CD)>EF.
如图,在四边形ABCD中,AB>CD,E,F分别是对角线BD,AC的中点,求证:$\frac{1}{2}$(AB+CD)>EF.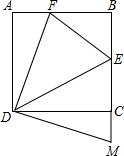 如图,正方形ABCD的边长为6,点E是BC的中点,点F在AB边上,BF=2AF,延长BC至点M,使得CM=AF.
如图,正方形ABCD的边长为6,点E是BC的中点,点F在AB边上,BF=2AF,延长BC至点M,使得CM=AF.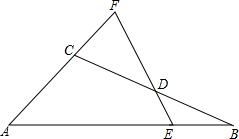 如图,△ABC中,D是BC边的中点,过点D的直线交AB于点E,交AC的延长线于点F,且BE=CF.
如图,△ABC中,D是BC边的中点,过点D的直线交AB于点E,交AC的延长线于点F,且BE=CF.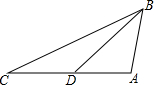 如图,在△ABC中,AC=2$\sqrt{2}$,D为边AC的中点,且∠CAB=105°,∠C=∠DBA,则BC的长度为$\sqrt{6}$$+\sqrt{2}$.
如图,在△ABC中,AC=2$\sqrt{2}$,D为边AC的中点,且∠CAB=105°,∠C=∠DBA,则BC的长度为$\sqrt{6}$$+\sqrt{2}$.