题目内容
14. 如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.
如图,矩形ABCD,AB=5,AD=8,E是AD上一动点,把△ABE沿BE折叠,当点A的对应点A′落在矩形ABCD的对称轴上时,折痕BE的长为$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.
分析 过A′作MN∥CD交AD于M,交BC于N,则直线MN是矩形ABCD 的对称轴,于是得到AM=BN=$\frac{1}{2}$AD=4,根据勾股定理得到A′N=$\sqrt{A′{B}^{2}-B{N}^{2}}$=3,于是求得A′M=2,再由勾股定理解得A′E=$\frac{5}{2}$,结论即可求出.
解答 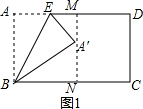 解:如图1,过A′作MN∥CD交AD于M,交BC于N,
解:如图1,过A′作MN∥CD交AD于M,交BC于N,
则直线MN是矩形ABCD 的对称轴,
∴AM=BN=$\frac{1}{2}$AD=4,
∵△ABE沿BE折叠得到△A′BE,
∴A′E=AE,A′B=AB=5,
∴A′N=$\sqrt{A′{B}^{2}-B{N}^{2}}$=3,
∴A′M=2,
∴A′E2=EM2+A′M2,
∴A′E2=(4-A′E)2+22,
解得:A′E=$\frac{5}{2}$,
∴AE=$\frac{5}{2}$,
在Rt△ABE中,BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\frac{5\sqrt{5}}{2}$,
如图2, 过A′作PQ∥AD交AB于P,交CD于Q,
过A′作PQ∥AD交AB于P,交CD于Q,
则直线PQ是矩形ABCD 的对称轴,
∴PQ⊥AB,AP=PB,AD∥PQ∥BC,
∴A′B=2PB,
∴∠PA′B=30°,
∴∠A′BC=30°,
∴∠EBA′=30°,
∴BE=$\frac{10\sqrt{3}}{3}$;
故答案为:$\frac{5\sqrt{5}}{2}$和$\frac{10\sqrt{3}}{3}$.
点评 本题考查了翻折变换-折叠问题,矩形的性质,勾股定理,正确理解折叠的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.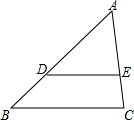 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
6.已知b>a>0.将分式$\frac{a}{b}$的分子、分母都分别加c(c>0),所得的分式$\frac{a+c}{b+c}$,则( )
| A. | $\frac{a}{b}>\frac{a+c}{b+c}$ | B. | $\frac{a}{b}<\frac{a+c}{b+c}$ | C. | $\frac{a}{b}=\frac{a+c}{b+c}$ | D. | 前三种均有可能 |
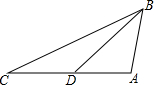 如图,在△ABC中,AC=2$\sqrt{2}$,D为边AC的中点,且∠CAB=105°,∠C=∠DBA,则BC的长度为$\sqrt{6}$$+\sqrt{2}$.
如图,在△ABC中,AC=2$\sqrt{2}$,D为边AC的中点,且∠CAB=105°,∠C=∠DBA,则BC的长度为$\sqrt{6}$$+\sqrt{2}$.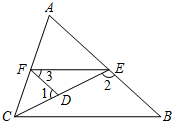 如图,已知∠1,∠2互为补角,且∠3=∠B,求证:∠AFE=∠ACB.
如图,已知∠1,∠2互为补角,且∠3=∠B,求证:∠AFE=∠ACB.