题目内容
1.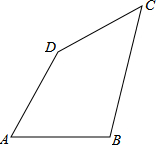 如图,四边形ABCD中,AB=AD=6cm,∠A=60°,BC=3$\sqrt{5}$cm,CD=3cm,求四边形ABCD的面积.
如图,四边形ABCD中,AB=AD=6cm,∠A=60°,BC=3$\sqrt{5}$cm,CD=3cm,求四边形ABCD的面积.
分析 连接BD,过D作DH⊥AB,首先证明△ABD是等边三角形,然后再证明△BDC是直角三角形,进而可求得面积.
解答 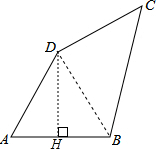 解:连接BD,过D作DH⊥AB,
解:连接BD,过D作DH⊥AB,
∵AB=AD=6cm,∠A=60°,
∴△ABD是等边三角形,
∴HD=AD×sin60°=3$\sqrt{3}$(cm),
∴BD=AD=6cm,
∵32+62=(3$\sqrt{5}$)2,
∴BD2+CD2=BC2,
∴△BDC是直角三角形,
∴四边形ABCD的面积=S△ADB+S△DCB=$\frac{1}{2}×$AB×DH+$\frac{1}{2}$DC×DB=$\frac{1}{2}×6$×$3\sqrt{3}$+$\frac{1}{2}×6×3$=9$\sqrt{3}$+9(cm2).
点评 此题主要考查了勾股定理逆定理,以及等边三角形的判定,关键是掌握有一个角是60°的等腰三角形是等边三角形.

练习册系列答案
相关题目
13.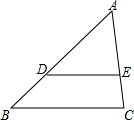 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
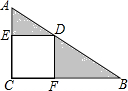 如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.
如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.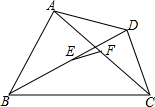 如图,在四边形ABCD中,AB>CD,E,F分别是对角线BD,AC的中点,求证:$\frac{1}{2}$(AB+CD)>EF.
如图,在四边形ABCD中,AB>CD,E,F分别是对角线BD,AC的中点,求证:$\frac{1}{2}$(AB+CD)>EF.