题目内容
4.半径为r的⊙O内切于△ABC,∠C=60°,AB=$\sqrt{3}$,求r的取值范围.分析 设AC=x,BC=y,根据S△ABC=$\frac{1}{2}$BC•AC•sinC=$\frac{1}{2}$(AB+AC+BC)r得到r=$\frac{\frac{\sqrt{3}}{2}xy}{x+y+\sqrt{3}}$①在直角三角形CFO中,根据三角函数和切线长定理得到CF=$\sqrt{3}$r=$\frac{1}{2}$(x+y-$\sqrt{3}$)于是得到x+y=2$\sqrt{3}$r+$\sqrt{3}$,x=2$\sqrt{3}$r+$\sqrt{3}$-y代入①,整理得到关于y的一元二次方程$\sqrt{3}$y2-3(2r+1)y+(4$\sqrt{3}$r2+4$\sqrt{3}$r)=0根据△≥0得到4r2+4r-3≥0即可得到结果.
解答 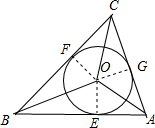 解:如图,设⊙O与△ABC的边相切于E,Q,F,连接OE,OF,OG,
解:如图,设⊙O与△ABC的边相切于E,Q,F,连接OE,OF,OG,
设AC=x,BC=y,
∵S△ABC=$\frac{1}{2}$BC•AC•sinC=$\frac{1}{2}$(AB+AC+BC)r
代入数据得到r=$\frac{\frac{\sqrt{3}}{2}xy}{x+y+\sqrt{3}}$①
又∵在直角三角形CFO中,CF=$\sqrt{3}$r=$\frac{1}{2}$(x+y-$\sqrt{3}$)
∴x+y=2$\sqrt{3}$r+$\sqrt{3}$,∴x=2$\sqrt{3}$r+$\sqrt{3}$-y
代入①,整理得到关于y的一元二次方程$\sqrt{3}$y2-3(2r+1)y+(4$\sqrt{3}$r2+4$\sqrt{3}$r)=0
∵△≥0
得到4r2+4r-3≥0
解得:-$\frac{3}{2}$≤r≤$\frac{1}{2}$
结合题意只能是0<r≤$\frac{1}{2}$,
故答案为0<r≤$\frac{1}{2}$.
点评 本题考查了三角形的内切圆和内心,三角形的面积公式,切线的性质,根据题意画出图形是解题的关键.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案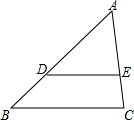 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
| A. | $\frac{a}{b}>\frac{a+c}{b+c}$ | B. | $\frac{a}{b}<\frac{a+c}{b+c}$ | C. | $\frac{a}{b}=\frac{a+c}{b+c}$ | D. | 前三种均有可能 |
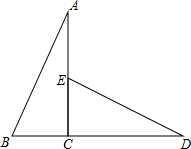 如图,已知△ABC≌△DEC,求证:BD-AE=2EC.
如图,已知△ABC≌△DEC,求证:BD-AE=2EC.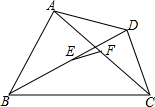 如图,在四边形ABCD中,AB>CD,E,F分别是对角线BD,AC的中点,求证:$\frac{1}{2}$(AB+CD)>EF.
如图,在四边形ABCD中,AB>CD,E,F分别是对角线BD,AC的中点,求证:$\frac{1}{2}$(AB+CD)>EF.