题目内容
6.在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套,当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?分析 设一个月内获得的利润为w元,根据题意得:w=(x-40)(-4x+480)然后利用配方法求最值.
解答 解:设销售单价为x(x≥60)元,销售量为y套,
可得:$y=240-\frac{x-60}{5}×20=-4x+480$;
设销售单价为x,一个月内获得的利润为w元,根据题意,得:
w=(x-40)y=(x-40)(-4x+480)
=-4x2+640x-19200
=-4(x-80)2+6400.
当x=80时,w的最大值为6400.
∴当销售单价为80元时,才能在一个月内获得最大利润,最大利润是6400元.
点评 本题考查了函数模型的选择与应用,考查了数学建模思想方法,关键是对题意的理解,是中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
16.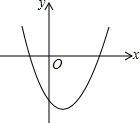 二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
 二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )
二次函数y=x2-2x-3的图象如图所示,下列说法中错误的是( )| A. | 函数图象与y轴的交点坐标是(0,-3) | |
| B. | 顶点坐标是(1,-3) | |
| C. | 函数图象与x轴的交点坐标是(3,0)、(-1,0) | |
| D. | 当x<0时,y随x的增大而减小 |
 如图,在△ABC中,∠ACB=90°,AB=5,AC=4,过点C作直线MC使得∠BCM=∠BAC,求点B到直线MC的距离.
如图,在△ABC中,∠ACB=90°,AB=5,AC=4,过点C作直线MC使得∠BCM=∠BAC,求点B到直线MC的距离.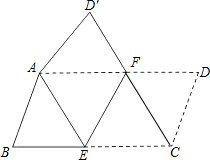 如图,将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D的落点记为点D′,折痕为EF,连接CF.
如图,将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D的落点记为点D′,折痕为EF,连接CF.  已知关于x的方程x2+(m-2)x+m-3=0.
已知关于x的方程x2+(m-2)x+m-3=0. 如图在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).
如图在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).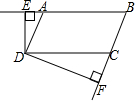 如图,在?ABCD中,DE⊥AB,DF⊥BC,∠EDF=120°,求∠B与∠BAD的度数.
如图,在?ABCD中,DE⊥AB,DF⊥BC,∠EDF=120°,求∠B与∠BAD的度数.