题目内容
11. 已知关于x的方程x2+(m-2)x+m-3=0.
已知关于x的方程x2+(m-2)x+m-3=0.(1)求证:方程x2+(m-2)x+m-3=0总有两个实数根;
(2)求证:抛物线y=x2+(m-2)x+m-3总过x轴上的一个定点;
(3)在平面直角坐标系xOy中,若(2)中的“定点”记作A,抛物线y=x2+(m-2)x+m-3与x轴的另一个交点为B,与y轴交于点C,且△OBC的面积小于或等于8,求m的取值范围.
分析 (1)求出△即可确定△≥0,进而得解;
(2)当y=0时,求出方程x2+(m-2)x+m-3=0的解,进而得证;
(3)根据题意,确定△OBC的面积小于或等于8,进而得解.
解答 解:(1)a=1,b=m-2,c=m-3,
△=b2-4ac=(m-2)2-4(m-3)
=m2-4m+4-4m+12
=m2-8m+16
=(m-4)2
∵(m-4)2≥0,
∴方程x2+(m-2)x+m-3=0总有两个实数根;
(2)x=$\frac{2-m±\sqrt{(m-4)^{2}}}{2}$=$\frac{2-m±(m-4)}{2}$
∴x1=-1,x2=-m+3,
∴抛物线y=x2+(m-2)x+m-3总过x轴上的一个定点(-1,0);
(3)∵抛物线y=x2+(m-2)x+m-3与x轴的另一个交点为B,与y轴交于点C,
∴B(3-m,0),C(0,m-3),
∴△OBC为等腰直角三角形,
∵△OBC的面积小于或等于8,
∴OB,OC小于或等于4,
∴3-m≤4或m-3≤4,
解得:-1≤m≤7,
∴-1≤m≤7,且m≠3.
点评 本题主要考查了一元二次方程的根的判别式,以及一元二次方程的求根公式,还考查了一元二次方程与二次函数之间的联系,是综合性比较强的题目,注意总结.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
1.下列英文字母是中心对称图形,但不是轴对称图形的是( )
| A. | N | B. | D | C. | W | D. | O |
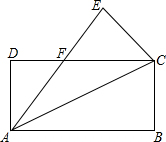 根据要求将下面题目改编成一道新题:如图,将矩形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,求证:折叠后的重叠部分(即△FAC)是等腰三角形
根据要求将下面题目改编成一道新题:如图,将矩形ABCD沿对角线AC折叠,点B落在E处,AE交DC于点F,求证:折叠后的重叠部分(即△FAC)是等腰三角形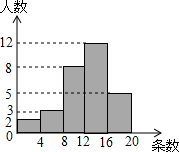 某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.
某项针对18岁~35岁的青年人每天发微博数量的调查中,随机对30名符合年龄的青年人开展每人“日均发微博条数”的调查,并绘制成如图所示的频数分布直方图,请根据频数分布直方图估计这30名青年人中“日均发微博条数”的平均数.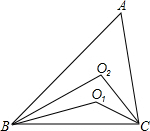 如图,△ABC中,∠A=60°,BO1、BO2三等分∠ABC,CO1、CO2三等分∠ACB.
如图,△ABC中,∠A=60°,BO1、BO2三等分∠ABC,CO1、CO2三等分∠ACB. 如图,AB∥DE,∠1=∠2.求证:AE∥DC.
如图,AB∥DE,∠1=∠2.求证:AE∥DC. 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是A′(5,2).
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是A′(5,2).