题目内容
7.在△ABC中,∠ABC=30°,∠BAC=70°.在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )| A. | 7条 | B. | 8条 | C. | 9条 | D. | 10条 |
分析 根据等腰三角形的判定,进行划分,即可解答.
解答 解:如图:
∴最多画8条,
故选:B.
点评 此题主要考查等腰三角形的判定以及三角形各角之间的关系,解决本题的关键是熟记等腰三角形的判定.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
17.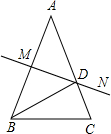 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )
 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )| A. | 0 | B. | 3 | C. | 2 | D. | 1 |
2.已知圆锥的底面半径为4cm,高为3cm,则圆锥的侧面积是( )
| A. | 20cm2 | B. | 20πcm2 | C. | 12πcm2 | D. | 10πcm2 |
19.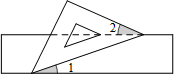 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
 如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )
如图,有一块含有45°角的直角三角板的两个顶点放在直尺的对边上,则∠1+∠2=( )| A. | 30° | B. | 45° | C. | 25° | D. | 15° |
16.下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )
| A. | 正三角形 | B. | 正四边形 | C. | 正五边形 | D. | 正六边形 |
 如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.
如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.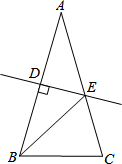 如图,在△ABC中,AB=AC,AB的垂直平分线交AC点E,垂足为点D,连接BE,若BE=BC,则∠EBC的度数为36°.
如图,在△ABC中,AB=AC,AB的垂直平分线交AC点E,垂足为点D,连接BE,若BE=BC,则∠EBC的度数为36°.