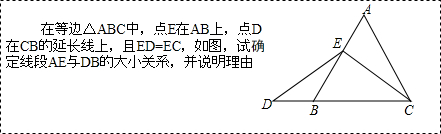
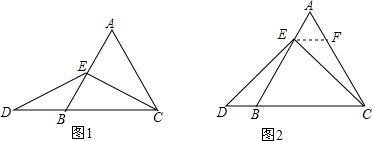
题目内容
17.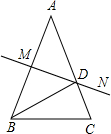 如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )
如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D、交AB于点M.下列结论:①BD是∠ABC的平分线;②△BCD是等腰三角形;③∠BDC=72°.正确的结论有几个( )| A. | 0 | B. | 3 | C. | 2 | D. | 1 |
分析 由AB=AC,∠A=36°,根据等腰三角形的性质,可求得∠ABC与∠C的度数,又由AB的中垂线MN交AC于点D、交AB于点M,可求得∠ABD的度数,继而可得BD是∠ABC的平分;△BCD是等腰三角形;∠BDC=72°.
解答 解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵AB的中垂线MN交AC于点D、交AB于点M,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠DBC=∠ABC-∠ABD=36°,
∴∠ABD=∠CBD,
即BD是∠ABC的平分线,故①正确;
∵∠BDC=∠A+∠ABD=72°,故③正确;
∴∠BDC=∠C,
∴BD=BC,
∴△BCD是等腰三角形;故②正确.
故选B.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等定理的应用.

练习册系列答案
相关题目
5.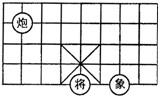 如图,象棋盘上“将”位于点(1,-2),则“炮”位于点( )
如图,象棋盘上“将”位于点(1,-2),则“炮”位于点( )
 如图,象棋盘上“将”位于点(1,-2),则“炮”位于点( )
如图,象棋盘上“将”位于点(1,-2),则“炮”位于点( )| A. | (-3,3) | B. | (3,3) | C. | (-2,1) | D. | (-2,3) |
12.在下列各电视台的台标图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
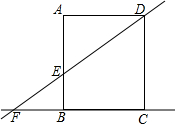 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.