题目内容
18. 如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.
如图,在?ABCD中,AC⊥AB,∠ABD=30°,AC交BD于O,AO=1,则BC的长为$\sqrt{7}$.
分析 由在?ABCD中,AC交BD于O,AO=1,根据平行四边形的性质,可求得AC的长,又由AC⊥AB,∠ABD=30°,可求得OB的长,然后由勾股定理求得AB与BC的长.
解答 解:∵在?ABCD中,AC交BD于O,AO=1,
∴AC=2OA=2,
∵在Rt△AOB中,AC⊥AB,∠ABD=30°,
∴OB=2OA=2,
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=$\sqrt{3}$,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 此题考查了平行四边形的性质、含30°角的直角三角形的性质以及勾股定理.注意利用勾股定理分别求得AB的长,利用平行四边形的性质求得AC的长.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
3.在一次“探究性学习”课中,老师设计如下数表:
(1)观察表格,根据规律在表中填空.
(2)用含自然数n(n>1)的代数式表示a、b、c,则a=n2-1,b=2n,c=n2+1.
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
| n | 2 | 3 | 4 | 5 | 6 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | 62-1 | … |
| b | 4 | 6 | 8 | 10 | 12 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | 62+1 | … |
(2)用含自然数n(n>1)的代数式表示a、b、c,则a=n2-1,b=2n,c=n2+1.
(3)猜想:以a,b,c为边的三角形是否为直角三角形?证明你的结论.
10.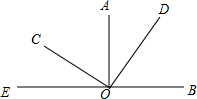 如图,已知AO⊥BE于O点,CO⊥DO于O点,∠BOC=α,则∠AOD的度数为( )
如图,已知AO⊥BE于O点,CO⊥DO于O点,∠BOC=α,则∠AOD的度数为( )
 如图,已知AO⊥BE于O点,CO⊥DO于O点,∠BOC=α,则∠AOD的度数为( )
如图,已知AO⊥BE于O点,CO⊥DO于O点,∠BOC=α,则∠AOD的度数为( )| A. | α-90° | B. | 2α-90° | C. | 180°-α | D. | 2α-180° |
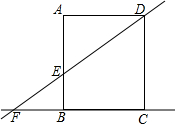 如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.
如图,在矩形ABCD中,AD=8,直线DE交直线AB于点E,交直线BC于F,AE=6且AE=2EB.则圆心在直线BC上,且与直线DE、AB都相切的⊙O的半径长为$\frac{3}{2}$或6.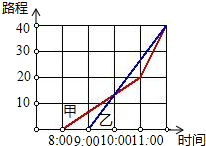 如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答: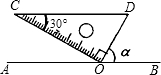 如图,一块含有60°三角板的顶点O在直线AB上,CD∥AB.则∠α=60度.
如图,一块含有60°三角板的顶点O在直线AB上,CD∥AB.则∠α=60度.