题目内容
20. 如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)
如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)
分析 因为△DCE是直角三角形,所以S△DCE=$\frac{1}{2}$•CE•CD,只要求出CE、CD即可解决问题.
解答 解: ∵正方形ABCD的面积是64m2,
∵正方形ABCD的面积是64m2,
∴CD=8cm,∠DCB=∠DCE=90°,
∵DC:EC=5:3,
∴EC=$\frac{24}{5}$cm,
∴S△DCE=$\frac{1}{2}$•CE•DC=$\frac{1}{2}$$•\frac{24}{5}$•8=$\frac{96}{5}$cm2.
点评 本题考查正方形的性质,直角三角形的面积等知识,解题时根据是灵活运用所学知识解决问题,所以基础题,中考常考题型.

练习册系列答案
相关题目
13.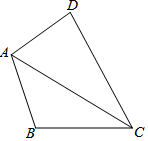 如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
 如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )| A. | 36 | B. | $36\sqrt{2}$ | C. | 72 | D. | $72\sqrt{2}$ |
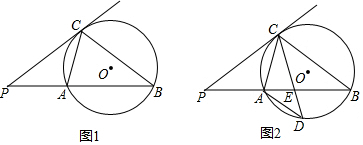
 如图,∠BAD=90°,射线AC平分∠BAE.
如图,∠BAD=90°,射线AC平分∠BAE. 如图,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠BED=150°,∠BDC=60°.求∠A的度数.
如图,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠BED=150°,∠BDC=60°.求∠A的度数.