题目内容
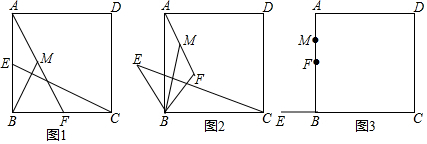
12. 如图,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠BED=150°,∠BDC=60°.求∠A的度数.
如图,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠BED=150°,∠BDC=60°.求∠A的度数.
分析 首先根据平行线的性质求出∠ABC的度数,再根据角平分线的性质求出∠CBD的度数,最后利用三角形内角和定理求出∠A的度数.
解答 解:∵DE∥CB,
∴∠BED+∠ABC=180°,
∵∠BED=150°,
∴∠ABC=30°,
∵BD是∠ABC的平分线,
∴∠CBD=$\frac{1}{2}$∠ABC=15°,
∵∠BDC=60°,
∴∠C=105°,
∴∠A=180°-∠ABC-∠C=45°.
点评 本题主要考查了三角形内角和定理以及平行线的性质,解题的关键是求出∠C的度数,此题难度不大.

练习册系列答案
相关题目
5. 有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
 有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )| A. | -2b | B. | -2a | C. | 2b | D. | 0 |
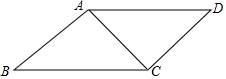 如图,在?ABCD中,AB=4cm,AC=6cm,∠BAC=90°,则BD之长为10cm.
如图,在?ABCD中,AB=4cm,AC=6cm,∠BAC=90°,则BD之长为10cm.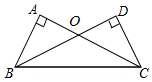 如图,∠A=∠D=90°,添加下列一个条件:①AB=CD;②AC=BD;③OB=OC;④∠ABC=∠BCD,其中能使△ABC≌△DCB成立的有( )
如图,∠A=∠D=90°,添加下列一个条件:①AB=CD;②AC=BD;③OB=OC;④∠ABC=∠BCD,其中能使△ABC≌△DCB成立的有( ) 如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)
如图中,正方形ABCD的面积是64m2,DC与EC的长度比是5:3,求三角形CDE的面积.(用比例解)