题目内容
11.已知关于x的分式方程$\frac{a+3}{x+1}$=1的解是非正数,则a的取值范围是a≤-2且a≠-3.分析 首先根据$\frac{a+3}{x+1}$=1,可得x=a+2;然后根据关于x的分式方程$\frac{a+3}{x+1}$=1的解是非正数,求出a的取值范围即可.
解答 解:∵$\frac{a+3}{x+1}$=1,
∴x=a+2,
∵关于x的分式方程$\frac{a+3}{x+1}$=1的解是非正数,
∴a+2≤0,
解得a≤-2,
又∵x=a+2≠-1,
∴a≠-3,
∴a的取值范围是:a≤-2且a≠-3.
故答案为:a≤-2且a≠-3.
点评 此题主要考查了分式方程的解,要熟练掌握,解答此题的关键是要明确:在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列图形既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.某中学随机调查了15名学生,了解他们一周在学校参加体育锻炼时间,列表如下:
则这15名同学一周在校参加体育锻炼时间的中位数和众数分别是6;6.
| 锻炼时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 2 | 6 | 5 | 2 |
1.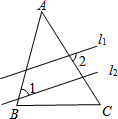 如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )
如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )
 如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )
如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )| A. | 35° | B. | 65° | C. | 85° | D. | 95° |
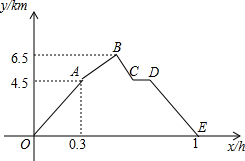 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km.下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的方,图中的折线OABCDE 表示y与x之间的函数关系,有下列说法正确的有( )个
从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km.下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的方,图中的折线OABCDE 表示y与x之间的函数关系,有下列说法正确的有( )个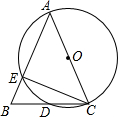 如图,在△ABC中,AB=AC=13,BC=10,以AC为直径画⊙O交BC于点D,交AB于点E,连接CE.
如图,在△ABC中,AB=AC=13,BC=10,以AC为直径画⊙O交BC于点D,交AB于点E,连接CE.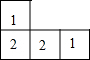 如图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是( )
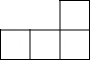
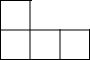
如图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是( )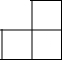

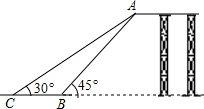 如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.
如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.