题目内容
8.已知x=2是关于x的一元二次方程x2+3x+m-2=0的一个根.(1)求m的值及方程的另一个根;
(2)若7-x≥1+m(x-3),求x的取值范围.
分析 (1)设方程另一个根为t,根据根与系数的关系得到2+t=-3,2t=m-2,先求出t,然后计算m的值;
(2)把m=-8代入7-x≥1+m(x-3)得到7-x≥1-8(x-3),然后解一元一次不等式即可.
解答 解:(1)设方程另一个根为t,
则2+t=-3,2t=m-2,
所以t=-5,m=-8,
即m的值为-8,方程的另一个根为-5;
(2)7-x≥1-8(x-3),
7-x≥1-8x+24,
8x-x≥1+24-7,
7x≥18,
所以x≥$\frac{18}{7}$.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.也考查了根与系数的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.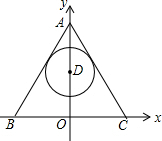 如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
 如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{3}$或3$\sqrt{3}$ | D. | 2$\sqrt{3}$或3$\sqrt{3}$ |
20.某中学随机调查了15名学生,了解他们一周在学校参加体育锻炼时间,列表如下:
则这15名同学一周在校参加体育锻炼时间的中位数和众数分别是6;6.
| 锻炼时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 2 | 6 | 5 | 2 |
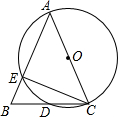 如图,在△ABC中,AB=AC=13,BC=10,以AC为直径画⊙O交BC于点D,交AB于点E,连接CE.
如图,在△ABC中,AB=AC=13,BC=10,以AC为直径画⊙O交BC于点D,交AB于点E,连接CE.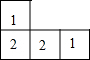 如图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是( )
如图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是( )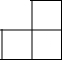

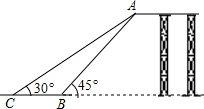 如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.
如图是某儿童游乐园滑梯的平面示意图,为了保障儿童玩滑梯时的安全性,游乐园计划改造滑梯的倾斜程度,使滑梯与地面的夹角由原来的45°减小到30°,已知原滑梯AB长为4米,求改造后滑梯AC的长及新、旧滑梯着地点C,B之间的距离.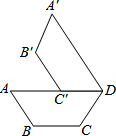 如图,在梯形ABCD中,AD∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于60度.
如图,在梯形ABCD中,AD∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于60度.