题目内容
18.若a+b=5,ab=4,则$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}$=$±\frac{1}{3}$.分析 利用(a-b)2=(a+b)2-4ab,求得a-b的值,再把所求代数式分母有理化后,代入计算.
解答 解:∵a+b=5,ab=4,
∴(a-b)2=(a+b)2-4ab=52-4×4=25-16=9,
∴a-b=±3,
∴$\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}$
=$\frac{a+b-2\sqrt{ab}}{a-b}$
=$\frac{5-2\sqrt{4}}{±3}$
=$±\frac{1}{3}$.
故答案为:$±\frac{1}{3}$.
点评 考查了分母有理化,此题主要利用了完全平方公式的变形(a-b)2=(a+b)2-4ab,以及分母有理化.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
8.下列计算正确的是( )
| A. | -$\frac{x}{y}$÷2y=-$\frac{x}{2}$ | B. | a2b•$\frac{a}{2b}$=$\frac{{a}^{3}}{2}$ | C. | (a2-b2)•$\frac{1}{b-a}$=a+b | D. | m3n2÷$\frac{{n}^{2}}{m}$•m=m3 |
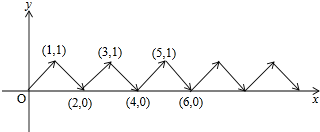 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,1),…,按这样的运动规律,经过第2016次运动后,点P运动的总长度是2016$\sqrt{2}$.
如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,1),…,按这样的运动规律,经过第2016次运动后,点P运动的总长度是2016$\sqrt{2}$.