题目内容
12.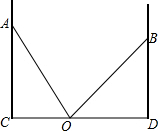 如图,已知AC、BD为数值的墙面,一架梯子从点O竖起,当靠在墙面AC上时,梯子的另一端落在点A处,此时∠AOC=60°,当靠在墙面BD上时,梯子的另一端落在点B处,此时∠BOD=45°,且OD=3$\sqrt{2}$米.
如图,已知AC、BD为数值的墙面,一架梯子从点O竖起,当靠在墙面AC上时,梯子的另一端落在点A处,此时∠AOC=60°,当靠在墙面BD上时,梯子的另一端落在点B处,此时∠BOD=45°,且OD=3$\sqrt{2}$米.(1)求梯子的长;
(2)求OC、AC的长.
分析 (1)先根据题意得出△BOD是等腰直角三角形,再由勾股定理即可得出OB的长;
(2)先根据直角三角形的性质求出OC的长,再由勾股定理即可得出AC的长.
解答 解:(1)∵由题意得,∠BDO=90°,∠BOD=45°,
∴∠B=45°.
∴OD=BD=3$\sqrt{2}$(米).
在Rt△OBD中,OB=$\sqrt{O{D}^{2}+B{D}^{2}}$=6(米),
∴梯子的长是6米;
(2)∵∠ACO=90°,∠AOC=60°,OA=OB=6米,
∴∠CAO=30°,
∴OC=$\frac{1}{2}$AO=3米.
在R△ACO中,AC=$\sqrt{A{O}^{2}-O{C}^{2}}$=$\sqrt{27}$=3$\sqrt{3}$米.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.计算(-a+2b)2-(-a-2b)2的结果是( )
| A. | -8ab | B. | -4ab | C. | 8ab | D. | 4ab |
1.下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行;(2)过一点有且只有一条直线与已知直线垂直;(3)在同一平面内,两条直线的位置关系只有相交,平行两种;(4)不相交的两条直线叫做平行线.
(1)过一点有且只有一条直线与已知直线平行;(2)过一点有且只有一条直线与已知直线垂直;(3)在同一平面内,两条直线的位置关系只有相交,平行两种;(4)不相交的两条直线叫做平行线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.如果∠A和∠B的两边分别平行,∠A=60°,那么∠B是( )
| A. | 60° | B. | 30°或120° | C. | 120° | D. | 60°或120° |
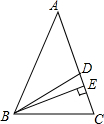 如图,在△ABC中,BD平分∠ABC,BE⊥AC,∠C>∠A,若∠C-∠A=20°,则∠DBE的度数是10°.
如图,在△ABC中,BD平分∠ABC,BE⊥AC,∠C>∠A,若∠C-∠A=20°,则∠DBE的度数是10°.