题目内容
17.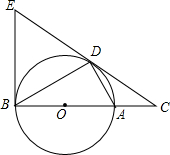 如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.(1)求证:CD是⊙O的切线;
(2)过点B作O的切线,交CD的延长线于点E,若BC=12,tan∠CDA=$\frac{2}{3}$,求BE的长.
分析 (1)连OD,OE,根据圆周角定理得到∠ADO+∠1=90°,而∠CDA=∠CBD,∠CBD=∠1,于是∠CDA+∠ADO=90°;
(2)根据切线的性质得到ED=EB,OE⊥BD,则∠ABD=∠OEB,得到tan∠CDA=tan∠OEB=$\frac{CB}{BE}=\frac{2}{3}$,易证Rt△CDO∽Rt△CBE,得到$\frac{CD}{CB}=\frac{OD}{BE}=\frac{OB}{BE}=\frac{2}{3}$,求得CD,然后在Rt△CBE中,运用勾股定理可计算出BE的长.
解答 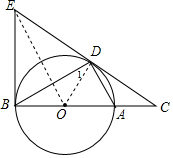 (1)证明:连OD,OE,如图,
(1)证明:连OD,OE,如图,
∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
(2)解:∵EB为⊙O的切线,ED是切线,
∴ED=EB,∵OB=OD,
∴OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA=$\frac{2}{3}$,
∴tan∠OEB=$\frac{OB}{BE}$=$\frac{2}{3}$,
∵Rt△CDO∽Rt△CBE,(1)证明:连OD,OE,如图,
∵AB为直径,
∴∠ADB=90°,即∠ADO+∠1=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠1,
∴∠1=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线;
∴$\frac{CD}{CB}$=$\frac{OD}{BE}$=$\frac{OB}{BE}$=$\frac{2}{3}$,
∴CD=$\frac{2}{3}$×12=8,
在Rt△CBE中,设BE=x,
∴(x+8)2=x2+122,
解得x=5.
即BE的长为5.
点评 本题考查了切线的判定与性质:过半径的外端点与半径垂直的直线是圆的切线;也考查了圆周角定理的推论以及三角形相似的判定与性质,熟练应用切线判定是解题的关键.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
| A. | 8 | B. | 9 | C. | 2$\sqrt{34}$或8 | D. | 2$\sqrt{34}$或9 |
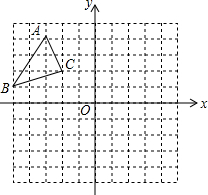 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(-3,4).
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(-3,4). 如图,在平面直角坐标系中,A(0,2),M(-4,0),点B从点M出发,速度为每秒k个单位,同时点P从原点O出发,速度为每秒1个单位,点B与点P都沿x轴正方向向右运动.设运动时间为t秒.动点Q在反比例函数y=$\frac{4}{x}$的图象上.
如图,在平面直角坐标系中,A(0,2),M(-4,0),点B从点M出发,速度为每秒k个单位,同时点P从原点O出发,速度为每秒1个单位,点B与点P都沿x轴正方向向右运动.设运动时间为t秒.动点Q在反比例函数y=$\frac{4}{x}$的图象上.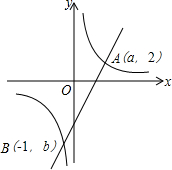 如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3.
如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3. 已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC, 如图,在?ABCD中,∠ABC的平分线交AD于点E,交CD的延长线于点F,
如图,在?ABCD中,∠ABC的平分线交AD于点E,交CD的延长线于点F,