题目内容
9.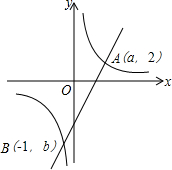 如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3.
如图,已知一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(a,2),B(-1,b)两点,当y1<y2时,x的取值范围是x<-1或0<x<3.
分析 先将A(a,2)代入y2=$\frac{6}{x}$,求出a的值,再求y1<y2时x的取值范围,即是求一次函数的值小于反比例函数的值的x的取值范围,根据图象可知就是求对应的一次函数的图象在反比例函数的图象下方的自变量的取值范围.
解答 解:∵反比例函数y2=$\frac{6}{x}$的图象经过A(a,2),
∴2=$\frac{6}{a}$,
∴a=3,
∴A(3,2).
∵一次函数y1=kx-4与反比例函数y2=$\frac{6}{x}$的图象都经过A(3,2),B(-1,b)两点,
∴当y1<y2时,x的取值范围是x<-1或0<x<3.
故答案为x<-1或0<x<3.
点评 本题考查了一次函数与反比例函数的交点问题,反比例函数图象上点的坐标特征,利用数形结合是解题的关键.

练习册系列答案
相关题目
20.二次根式$\frac{1}{\sqrt{x-1}}$中,x的取值范围是( )
| A. | x≠1 | B. | x≥1 | C. | x>1 | D. | x≤1 |
18.一个盒子里有完全相同的四个小球,球上分别标有-2,0,1,2,随机从盒子里摸出两个小球,上面的数字之和不为0的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
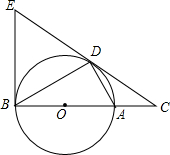 如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD. 如图,是10×8的网格,网格中每个小正方形的边长均为1,线段AB的端点都在小正方形的顶点上,
如图,是10×8的网格,网格中每个小正方形的边长均为1,线段AB的端点都在小正方形的顶点上, 如图,∠1+∠2=180°,∠3=∠B,那么∠EDG与∠DGB相等吗?
如图,∠1+∠2=180°,∠3=∠B,那么∠EDG与∠DGB相等吗?