题目内容
6. 已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,(1)求证:四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求tan∠BCD的值.
分析 (1)利用线段垂直平分线的性质得出AB=CB,AD=CD,进而得出AF∥BD,AB∥FD即可得出答案;
(2)利用勾股定理得出FG的长,再利用锐角三角函数关系得出答案.
解答  (1)证明:∵BD垂直平分AC,
(1)证明:∵BD垂直平分AC,
∴AB=CB,AD=CD,
∴∠BAC=∠BCA,∠DAC=∠DCA.
即∠BAD=∠BCD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
又∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形;
(2)解:连接FB,交AD于点G,
∵AF=DF,
∴平行四边形ABDF是菱形
∴∠DGF=90°,DG=$\frac{1}{2}$AD=3,
∴FG=$\sqrt{D{F}^{2}-D{G}^{2}}$=4,
∴tan∠FDG=$\frac{FG}{DG}$=$\frac{4}{3}$,
∴tan∠BCD=$\frac{4}{3}$.
点评 此题主要考查了平行四边形的判定以及菱形的判定和勾股定理等知识,得出平行四边形ABDF是菱形是解题关键.

练习册系列答案
相关题目
18.一个盒子里有完全相同的四个小球,球上分别标有-2,0,1,2,随机从盒子里摸出两个小球,上面的数字之和不为0的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
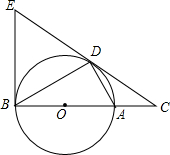 如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD. 如图,∠1+∠2=180°,∠3=∠B,那么∠EDG与∠DGB相等吗?
如图,∠1+∠2=180°,∠3=∠B,那么∠EDG与∠DGB相等吗? 如图,⊙O的直径AB交弦CD于点P,请你添加一个条件:AP⊥CD,使得CP=DP.
如图,⊙O的直径AB交弦CD于点P,请你添加一个条件:AP⊥CD,使得CP=DP.