题目内容
7. 如图,在?ABCD中,∠ABC的平分线交AD于点E,交CD的延长线于点F,
如图,在?ABCD中,∠ABC的平分线交AD于点E,交CD的延长线于点F,(1)请写出图中的等腰三角形,并证明其中一个三角形是等腰三角形;
(2)若E恰好是AD的中点,AB长为4,∠ABC=60°,求△BCF的面积.
分析 (1)由在?ABCD中,∠ABC的平分线交AD于点E,易证得等腰三角形有:△EFD、△ABE、△BCF;
(2)首先过点A作AH⊥BC于点H,可求得AH与AD的长,易证得△ABE≌△DFE(AAS),即可得S△BCF=S?ABCD.
解答 解:(1)等腰三角形有:△EFD、△ABE、△BCF.
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BF平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
即△ABE是等腰三角形; (2)过点A作AH⊥BC于点H,
(2)过点A作AH⊥BC于点H,
∵AB=4,∠ABC=60°,
∴AH=2$\sqrt{3}$,AD=2AE=2AB=8,
在?ABCD中,AB∥CD,
∴∠A=∠ADF,∠ABE=∠F,
又∵E恰好是AD的中点,
∴AE=DE,
在△ABE和△DFE中,
$\left\{\begin{array}{l}{∠A=∠ADF}\\{∠ABE=∠F}\\{AE=DE}\end{array}\right.$,
∴△ABE≌△DFE(AAS),
∴S△BCF=S?ABCD=8×2$\sqrt{3}$=16$\sqrt{3}$.
点评 此题考查了平行四边形的性质、等腰三角形的判定与性质以及全等三角形的判定与性质.注意掌握辅助线的作法.

练习册系列答案
相关题目
18.一个盒子里有完全相同的四个小球,球上分别标有-2,0,1,2,随机从盒子里摸出两个小球,上面的数字之和不为0的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
12.已知0≤x<$\frac{1}{2}$,那么函数y=-2x2+8x-6的最大值是( )
| A. | -6 | B. | -2.5 | C. | 2 | D. | 不能确定 |
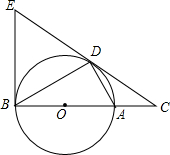 如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.
如图,点D为⊙O上的一点,点C在直径BA的延长线上,并且∠CDA=∠CBD.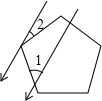 如图,一束平行太阳光照射到正五边形上,若∠1=45°,则∠2=27°.
如图,一束平行太阳光照射到正五边形上,若∠1=45°,则∠2=27°.