题目内容
18.关于x的一元二次方程x2+(2m+1)x+m2-1=0有两个不相等的实数根.(1)求m的取值范围;
(2)当m取满足条件的最小整数时,求方程的解.
分析 (1)根据方程有两个不相等的实数根根,则根的判别式△=b2-4ac>0,建立关于m的不等式,求出m的取值范围;
(2)得到m的最小整数,利用因式分解法解一元二次方程即可.
解答 解:(1)∵一元二次方程x2+(2m+1)x+m2-1=0有两个不相等的实数根,
∴△=(2m+1)2-4(m2-1)=4m+5>0,
∴m>-$\frac{5}{4}$;
(2)m满足条件的最小值为m=-1,
此时方程为x2-x=0,
解得x1=0,x2=1.
点评 考查了根的判别式,总结:一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
9.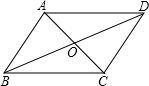 如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应增加的条件是( )
如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应增加的条件是( )
 如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应增加的条件是( )
如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应增加的条件是( )| A. | AB=CD | B. | ∠BAD=∠DCB | C. | AC=BD | D. | ∠ABC+∠BAD=180° |
6. 在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
(1)表格中a的值为100,b的值为125.
(2)扇形统计图中表示获得一等奖的扇形的圆心角为72度.
(3)估计全市有多少名学生获得三等奖?
 在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.| 获奖等级 | 频数 |
| 一等奖 | a |
| 二等奖 | b |
| 三等奖 | 275 |
(2)扇形统计图中表示获得一等奖的扇形的圆心角为72度.
(3)估计全市有多少名学生获得三等奖?
3.已知$\sqrt{a-2}$+(b+$\frac{1}{2}$)2=0,则a2016b2017的值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
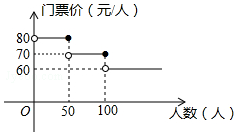 我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
 如图,在平面直角坐标系中有两点A,B
如图,在平面直角坐标系中有两点A,B