题目内容
18. 如图,在平面直角坐标系中有两点A,B
如图,在平面直角坐标系中有两点A,B(1)尺规作图,在x轴上找一点C,使得AC+BC最小:(尺规作图,不写作法,保留作图痕迹);
(2)若A的坐标为(-2,1),B的坐标为(3,5)在x轴上找一点C,使得AC+BC最小,求点C的坐标.
分析 (1)先作出点A关于x轴的对称点A′,再连结A′B交x轴于点C即可;
(2)利用关于x轴对称点坐标关系得出A′的坐标,根据待定系数法可求A′B的解析式,再把y=0代入可求点C的坐标即可.
解答 解:(1)如图所示:
(2)点A关于x轴的对称点A′(-2,-1),
设直线A′B的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-2k+b=-1}\\{3k+b=5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{6}{5}}\\{b=\frac{7}{5}}\end{array}\right.$,
则直线A′B的解析式为y=$\frac{6}{5}$x+$\frac{7}{5}$,
当y=0时,$\frac{6}{5}$x+$\frac{7}{5}$=0,解得x=-$\frac{7}{6}$.
故点C的坐标为(-$\frac{7}{6}$,0).
点评 此题主要考查了关于坐标轴对称点的性质以及轴对称-最短路线问题,根据轴对称的性质得出对称点的坐标是解题关键.

练习册系列答案
相关题目
9.下列各式中,能用平方差公式分解因式的是( )
| A. | 2x3-1 | B. | 1-x2 | C. | x2+1 | D. | -x2-1 |
6.地球与月球之间的平均距离是38.4万千米,数据“38.4万”用科学记数法表示为( )
| A. | 38.4×104 | B. | 3.84×105 | C. | 3.84×106 | D. | 3.84×104 |
13. 如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )
如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )
 如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )
如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
3.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (ab)2=ab2 | C. | (a2)4÷(a3)2=a2 | D. | (-a2)3=-a8 |
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上,将△ABC向左平移2格,再向上平移4格.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上,将△ABC向左平移2格,再向上平移4格.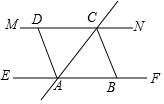 已知EF∥MN,直线AC交EF、MN于点A、C,作∠ACN的角平分线于点B,作∠CAE的角平分线交MN于点D.
已知EF∥MN,直线AC交EF、MN于点A、C,作∠ACN的角平分线于点B,作∠CAE的角平分线交MN于点D.