��Ŀ����
17����ͼ1����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=5��BD=10��ƽ���ı���ABCD�����Ϊ24������COD�Ƶ�D����ʱ�뷽����ת�õ���C1O D1������AC1��BD1��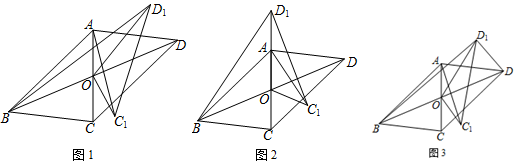
��1����֤����AOC1�ס�BOD1��
��2������COD��ת��OD1���A�غ�ʱ�����AOC1�������
��3����ͼ3������DD1��
�����BDD1����������ֵΪ25����ֱ����գ�
�ڵ���ת����C1���B֮��ľ������ʱ�����ʱBD1�ij���
���� ��1���������߳ɱ����н���ȵ������������Ƽ���֤����
��2����ͼ2�У���C1H��AC��H����${S}_{��{D}_{1}O{C}_{1}}$=$\frac{1}{4}$��24=$\frac{1}{2}$��OD1��C1H�����C1H=$\frac{12}{5}$������${S}_{��AO{C}_{1}}$=$\frac{1}{2}$•OA•C1H���㼴�ɽ�����⣻
��3������ͼ3�У���OD1��BDʱ����BDD1�����������ֵ=$\frac{1}{2}$•BD•OD1��
����ͼ4�У���D1H��BD��H����$\frac{1}{2}$•OC1•D1H=$\frac{1}{4}$��24�����D1H=$\frac{24}{5}$����Rt��OD1H�У�OH=$\sqrt{O{{D}^{2}}_{1}-{D}_{1}{H}^{2}}$=$\frac{7}{5}$���Ƴ�BH=OB-OH=$\frac{18}{5}$����Rt��BHD1�У�BD1=$\sqrt{{D}_{1}{H}^{2}+B{H}^{2}}$=6��
��� ��1��֤������ͼ1�У�
�ߡ�COC1=��DOD1��
���AOC1=��BOD1��
���ı���ABCD��ƽ���ı��Σ�
��OA=OC=OC1��OB=OD=OD1��
��$\frac{O{C}_{1}}{O{D}_{1}}$=$\frac{OA}{OB}$��
���AOC1�ס�BOD1��
��2���⣺��ͼ2�У���C1H��AC��H��
��${S}_{��{D}_{1}O{C}_{1}}$=$\frac{1}{4}$��24=$\frac{1}{2}$��OD1��C1H��
��C1H=$\frac{12}{5}$��
��${S}_{��AO{C}_{1}}$=$\frac{1}{2}$•OA•C1H=$\frac{1}{2}$��$\frac{5}{2}$��$\frac{12}{5}$=3��
��3������ͼ3�У���OD1��BDʱ����BDD1�����������ֵ=$\frac{1}{2}$•BD•OD1=$\frac{1}{2}$��10��5=25��
�ʴ�Ϊ25��
����ͼ4�У���D1H��BD��H��
��$\frac{1}{2}$•OC1•D1H=$\frac{1}{4}$��24��
��D1H=$\frac{24}{5}$��
��Rt��OD1H��OH=$\sqrt{O{{D}^{2}}_{1}-{D}_{1}{H}^{2}}$=$\frac{7}{5}$��
��BH=OB-OH=$\frac{18}{5}$��
��Rt��BHD1��BD1=$\sqrt{{D}_{1}{H}^{2}+B{H}^{2}}$=6��
���� ���⿼�������������ۺ��⡢ƽ���ı��ε����ʡ���ֱ�������Ρ����ɶ��������������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ�����ֱ�������ν�����⣬�����п�ѹ���⣮

 ��У����ϵ�д�
��У����ϵ�д�| A�� | 6 | B�� | 12 | C�� | ��12 | D�� | ��6 |
| A�� | 2x3-1 | B�� | 1-x2 | C�� | x2+1 | D�� | -x2-1 |
| A�� | 38.4��104 | B�� | 3.84��105 | C�� | 3.84��106 | D�� | 3.84��104 |
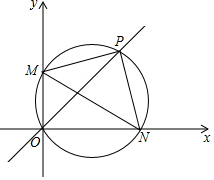 ��ͼ��M��N�ֱ�Ϊֱ������ϵx��y�����������㣬��M��N��ԭ��O�����Բ��ֱ��y=x���ڵ�P��
��ͼ��M��N�ֱ�Ϊֱ������ϵx��y�����������㣬��M��N��ԭ��O�����Բ��ֱ��y=x���ڵ�P�� ��ղ��������������
��ղ�������������� ��ͼ����ÿ��С�����α߳�Ϊ1�ķ���ֽ�У���ABC�Ķ��㶼�ڷ���ֽ����ϣ�����ABC����ƽ��2��������ƽ��4��
��ͼ����ÿ��С�����α߳�Ϊ1�ķ���ֽ�У���ABC�Ķ��㶼�ڷ���ֽ����ϣ�����ABC����ƽ��2��������ƽ��4��