题目内容
6. 在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.| 获奖等级 | 频数 |
| 一等奖 | a |
| 二等奖 | b |
| 三等奖 | 275 |
(2)扇形统计图中表示获得一等奖的扇形的圆心角为72度.
(3)估计全市有多少名学生获得三等奖?
分析 (1)由一等奖学生数及其所占百分比求得被调查学生总数,根据各组频数之和等于总数即可得a;
(2)用360°乘以获得一等奖所对应百分比即可得;
(3)用全州获奖学生总数乘以样本中获三等奖所占比例.
解答 解:(1)抽取的总人数是275÷(1-25%-20%)=500,
则a=500×20%=100;b=500×25%=125.
故答案是:100,125;
(2)获得一等奖的扇形的圆心角是360°×20%=72°,
故答案是:72;
(3)80000×(1-25%-20%)=44000(人),
答:估计全市有44000名学生获得三等奖.
点评 本题主要考查频数分布表与扇形统计图及用样本估计总体,从统计图表中获取解题所需信息是解题的关键.

练习册系列答案
相关题目
16.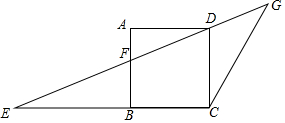 如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.
如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.
(1)求证:△FAD∽△FBE;
(2)若正方形的边长为5,EF:FD:DG=2:1:1,求△ECG的面积.
 如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.
如图,正方形ABCD的边BC恰好在△ECG边EC上,点D在边EG上,AB与EG交于点F.(1)求证:△FAD∽△FBE;
(2)若正方形的边长为5,EF:FD:DG=2:1:1,求△ECG的面积.
17.若4a2-kab+9b2是完全平方式,则常数k的值为( )
| A. | 6 | B. | 12 | C. | ±12 | D. | ±6 |
14.若(x-p)(x-2)=x2+2p,则p的值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
11.已知关于x的分式方程$\frac{2x+m}{x-2}$=3的解是正数,则m可能的取值为( )
| A. | -7 | B. | -6 | C. | -5 | D. | -4 |
6.地球与月球之间的平均距离是38.4万千米,数据“38.4万”用科学记数法表示为( )
| A. | 38.4×104 | B. | 3.84×105 | C. | 3.84×106 | D. | 3.84×104 |
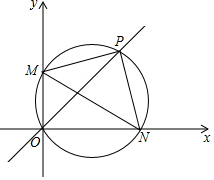 如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,
如图:M、N分别为直角坐标系x、y正半轴上两点,过M、N和原点O三点的圆和直线y=x交于点P,