题目内容
4. 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{k}{x}$(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,那么图中阴影部分的面积之和为$\frac{49}{18}$,则k的值为4.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{k}{x}$(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,那么图中阴影部分的面积之和为$\frac{49}{18}$,则k的值为4.
分析 先根据反比例函数比例系数k的几何意义得到S△OB1C1=S△OB2C2=S△OB3C3=$\frac{1}{2}$|k|=$\frac{1}{2}$k,再根据相似三角形的面积比等于相似比的平方,得到用含k的代数式表示3个阴影部分的面积之和,然后根据三个阴影部分的面积之和为$\frac{49}{18}$,列出方程,解方程即可求出k的值.
解答 解:根据题意可知,S△OB1C1=S△OB2C2=S△OB3C3=$\frac{1}{2}$|k|=$\frac{1}{2}$k,
∵OA1=A1A2=A2A3,A1B1∥A2B2∥A3B3∥y轴,
设图中阴影部分的面积从左向右依次为S1,S2,S3,
则S1=$\frac{1}{2}$k,
∵OA1=A1A2=A2A3,
∴S2:S△OB2C2=1:4,S3:S△OB3C3=1:9,
∴S2=$\frac{1}{8}$k,S3=$\frac{1}{18}$k,
∴$\frac{1}{2}$k+$\frac{1}{8}$k+$\frac{1}{18}$k=$\frac{49}{18}$,
解得:k=4.
故答案为:4.
点评 此题综合考查了反比例函数的性质、反比例函数系数k的几何意义等知识;此题难度稍大,综合性比较强,注意反比例函数上的点向x轴与y轴引垂线形成的矩形面积等于反比例函数的比例系数|k|.

练习册系列答案
相关题目
12.在因此女子体操比赛中,8名运动员的年龄(单位:岁)分别为:14,12,12,15,14,15,14,16.这组数据的中位数和方差分别为( )
| A. | 14和2 | B. | 14.5和1.75 | C. | 14和1.75 | D. | 15和2 |
19.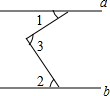 如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
 如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )| A. | 20° | B. | 80° | C. | 100° | D. | 90° |
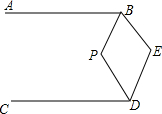 如图,已知AB∥CD,∠E=n°,分别作∠ABE与∠CDE的角平分线交于点P,则∠P的度数为(180-$\frac{n}{2}$)°(用含n的代数式表示).
如图,已知AB∥CD,∠E=n°,分别作∠ABE与∠CDE的角平分线交于点P,则∠P的度数为(180-$\frac{n}{2}$)°(用含n的代数式表示).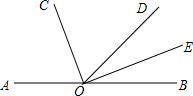 如图,∠AOD与∠BOD互为补角,射线OC、OE分别平分∠AOD和∠BOD.
如图,∠AOD与∠BOD互为补角,射线OC、OE分别平分∠AOD和∠BOD.
