题目内容
19.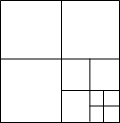 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.
分析 可以发现,大正方形的面积为1,进行第一次操作后右下角的小正方形的面积为$\frac{1}{4}$,以此类推即可发现第5次操作后右下角小正方形的面积为$(\frac{1}{4})^{5}$进而得解.
解答 解:大正方形的面积为1,
进行第一次操作后右下角的小正方形的面积为$\frac{1}{4}$;
进行第2次操作后右下角的小正方形的面积为$(\frac{1}{4})^{2}$;
进行第3次操作后右下角的小正方形的面积为$(\frac{1}{4})^{3}$;
进行第4次操作后右下角的小正方形的面积为$(\frac{1}{4})^{4}$;
进行第5次操作后右下角的小正方形的面积为$(\frac{1}{4})^{5}$,
故答案为:$(\frac{1}{4})^{5}$.
点评 本题考查了规律型:图形的变化类,通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.不等式$\frac{x-1}{2}-\frac{x-2}{4}$>1去分母后得( )
| A. | 2(x-1)-x-2>1 | B. | 2(x-1)-x+2>1 | C. | 2(x-1)-x-2>4 | D. | 2(x-1)-x+2>4 |
9.下列运算正确的是( )
| A. | x3-3x2=-2x | B. | (-$\frac{1}{3}{x}^{3}$)2=$\frac{1}{9}$x6 | C. | 6x3÷2x-2=3x | D. | (2x-4)2=4x2-16 |
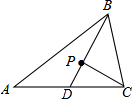 如图,BD是△ABC的中线,点P是△ABC的重心,连接PC.
如图,BD是△ABC的中线,点P是△ABC的重心,连接PC.