题目内容
10.已知x=1是一元二次方程ax2+bx-40=0的一个解,且a≠b,(1)求$\frac{{{a^2}-{b^2}}}{2a-2b}$的值.
(2)求(a-b)0+(a+b)-2的值.
分析 (1)先根据一元二次方程的解得到a+b=40,然后把原式进行化简得到$\frac{{{a^2}-{b^2}}}{2a-2b}$=$\frac{1}{2}$(a+b),再利用整体代入的方法计算;
(2)根据零指数幂的意义得出(a-b)0=1,将a+b=40代入利用负整数指数幂的意义计算即可.
解答 解:(1)把x=1代入方程得a+b-40=0,即a+b=40,
所以$\frac{{{a^2}-{b^2}}}{2a-2b}$=$\frac{(a+b)(a-b)}{2(a-b)}$=$\frac{1}{2}$(a+b)=$\frac{1}{2}$×40=20;
(2)∵a≠b,
∴a-b≠0,
∴(a-b)0+(a+b)-2=1+$\frac{1}{4{0}^{2}}$=1$\frac{1}{1600}$.
点评 本题考查了一元二次方程的解的意义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了零指数幂、负整数指数幂的意义.注意解题中的整体代入思想.

练习册系列答案
相关题目
15. 如图是直棱柱的表面展开图,AB=3cm,AC=5cm,且四边形DHGF为正方形,则它的侧面积是( )
如图是直棱柱的表面展开图,AB=3cm,AC=5cm,且四边形DHGF为正方形,则它的侧面积是( )
 如图是直棱柱的表面展开图,AB=3cm,AC=5cm,且四边形DHGF为正方形,则它的侧面积是( )
如图是直棱柱的表面展开图,AB=3cm,AC=5cm,且四边形DHGF为正方形,则它的侧面积是( )| A. | 60cm2 | B. | 72cm2 | C. | 50cm2 | D. | 53cm2 |
2.若-x2y=2,则-xy(x5y2-x3y+2x)的值为( )
| A. | 16 | B. | 12 | C. | 8 | D. | 0 |
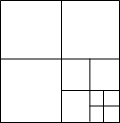 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.