题目内容
9.(1)①当a=2,b=1时,分别求出式子a2-2ab+b2与(a-b)2的值;②当a=3,b=-4时,再分别求出式子a2-2ab+b2与(a-b)2的值;
(2)由(1)①②的计算结果中,你发现什么规律吗?请你将这个规律用式子表示出来
(3)利用(2)表示规律的式子,求20132-4026+1的值.
分析 (1)分别把a、b的值代入代数式进行计算即可得解;
(2)根据计算结果相等可得两个代数式相等;
(3)把4026写成2×2013×1,然后根据(2)的规律进行计算即可得解.
解答 解:(1)①a2-2ab+b2=22-2×2×1+12=4-4+1=1,
(a-b)2=(2-1)2=1;
②a2-2ab+b2=32-2×3×(-4)+(-4)2=9+24+16=49,
(a-b)2=[3-(-4)]2=49;
(2)规律:a2-2ab+b2=(a-b)2;
(3)20132-4026+1=20132-2×2013×1+1=(2013-1)2=20122.
点评 本题考查了代数式求值,是基础题,准确计算是解题的关键.

练习册系列答案
相关题目
17.如图是由一些棱长为1厘米的小正方体按一定规律组成的立体图形.第9个图中小正方体的个数及第9个图中立体图形的表面积分别是( )


| A. | 29个;118平方厘米 | B. | 28个;116平方厘米 | ||
| C. | 27个;114平方厘米 | D. | 26个;112平方厘米 |
 将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示第m排,从左到右第n个数,如(3,2)表示正整数5,(4,3)表示正整数9,则(100,16)表示的正整数是4966.
将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示第m排,从左到右第n个数,如(3,2)表示正整数5,(4,3)表示正整数9,则(100,16)表示的正整数是4966.
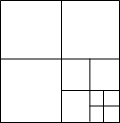 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.