题目内容
14.已知a,b,c是△ABC三边的长,化简|a-b+c|+|c-a-b|=2a.分析 由“三角形的两边之和大于第三边”可得出“a+c>b,a+b>c”,再根据绝对值的性质去绝对值符号,最后利用整式加减法的运算法则即可得出结论.
解答 解:∵a,b,c是△ABC三边的长,
∴a+c>b,a+b>c,
∴|a-b+c|+|c-a-b|=a+c-b+(a+b-c)=2a.
故答案为:2a.
点评 本题考查了整式的加减、绝对值以及三角形的三边关系,解题的关键是以及三角形的三边关系得出“a+c>b,a+b>c”.本题属于基础题,难度不大,解决该题型题目时,依据三角形的三边关系结合绝对值的性质对整式进行化简求值.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
2.若-x2y=2,则-xy(x5y2-x3y+2x)的值为( )
| A. | 16 | B. | 12 | C. | 8 | D. | 0 |
3.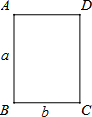 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙 S甲=S乙 | B. | V甲<V乙 S甲=S乙 | ||
| C. | V甲=V乙 S甲=S乙 | D. | V甲>V乙 S甲<S乙 |
 将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示第m排,从左到右第n个数,如(3,2)表示正整数5,(4,3)表示正整数9,则(100,16)表示的正整数是4966.
将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示第m排,从左到右第n个数,如(3,2)表示正整数5,(4,3)表示正整数9,则(100,16)表示的正整数是4966.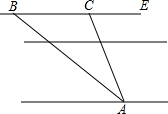 在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次测量活动中,同学们想测量某高速公路的宽度.如图,他们在该高速公路的东侧选定一广告牌A,并在西侧防护带的外沿B处观察,此时视线BA与外沿BE所成的夹角是30°,沿外沿BE向北走了8米到C处,再观察A,此时视线CA与外沿所成的夹角∠ACE=60°,已纪该高速公路西侧防护带宽1米.求此高速公路的宽约为多少米.(结果精确到1米.参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)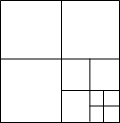 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.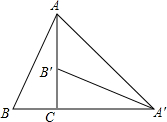 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结AA′,若∠B=70°,则∠B′A′A的度数是25°.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结AA′,若∠B=70°,则∠B′A′A的度数是25°. 如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.