题目内容
11.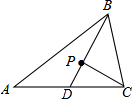 如图,BD是△ABC的中线,点P是△ABC的重心,连接PC.
如图,BD是△ABC的中线,点P是△ABC的重心,连接PC.(1)写出图中的所有三角形△ABC、△ABD、△CBD、△BPC、△DPC;
(2)若延长CP交AB于点E,BC=5cm,AC=7cm,AB为整数,求整数AE的长.
分析 (1)根据图形和三角形的概念数出所有的三角形即可;
(2)根据三角形三边关系求出AB的值,根据重心的概念解答即可.
解答 解:(1)图中是三角形有△ABC、△ABD、△CBD、△BPC、△DPC,
故答案为:△ABC、△ABD、△CBD、△BPC、△DPC;
(2)延长CP交AB于点E,
∵BC=5cm,AC=7cm,
∴7cm-5cm<AB<7cm+5cm,即2cm<AB<12cm,又AB为整数,
∴AB=3cm、4cm、5cm、6cm、7cm、8cm、9cm、10cm、11cm,
∵点P是△ABC的重心,
∴点E是AB的中点,即AE=$\frac{1}{2}$AB,又AE为整数,
∴AB=2cm、3cm、4cm、5cm.
点评 本题考查的是三角形的重心的概念和性质,三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.

练习册系列答案
相关题目
2.若-x2y=2,则-xy(x5y2-x3y+2x)的值为( )
| A. | 16 | B. | 12 | C. | 8 | D. | 0 |
16.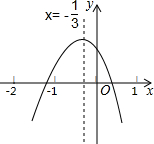 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:
①ab>0;
②a+b+c<0;
③b+2c>0;
④点(-3,m),(6,n)都在抛物线上,则有m<n;
你认为其中正确的有( )
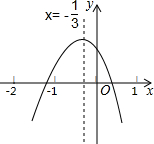 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,下面四条信息:①ab>0;
②a+b+c<0;
③b+2c>0;
④点(-3,m),(6,n)都在抛物线上,则有m<n;
你认为其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
3.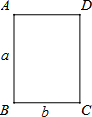 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙 S甲=S乙 | B. | V甲<V乙 S甲=S乙 | ||
| C. | V甲=V乙 S甲=S乙 | D. | V甲>V乙 S甲<S乙 |
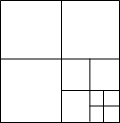 连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.
连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…,重复这样的操作,则5次操作后右下角的小正方形面积是$(\frac{1}{4})^{5}$.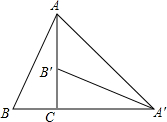 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结AA′,若∠B=70°,则∠B′A′A的度数是25°.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结AA′,若∠B=70°,则∠B′A′A的度数是25°.