题目内容
17.阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=$\frac{k}{x}$交于A(1,3)和B(-3,-1)两点.观察图象可知:当x=-3或1时,y1=y2.
(1)通过观察函数的图象,可以得到不等式ax+b>$\frac{k}{x}$的解集x>1或-3<x<0.
(2)参考观察函数的图象方法,解决问题:关于x的不等式x2+a-$\frac{4}{x}$<0(a>0)只有一个整数解,则a的取值范围0<a<3.
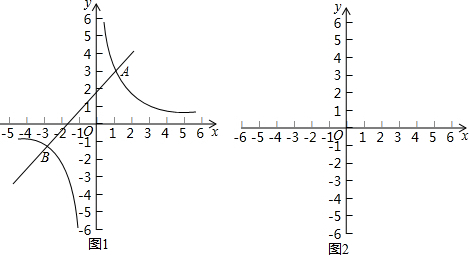
分析 (1)根据图象中两个交点的坐标可以得出不等式的解集;
(2)根据不等式确定两个函数:y=$\frac{4}{x}$和y=x2+a,画图象观察得出结论.
解答  解:(1)由图象得:
解:(1)由图象得:
不等式ax+b>$\frac{k}{x}$的解集为:x>1或-3<x<0;
(2)x2+a-$\frac{4}{x}$<0,
x2+a<$\frac{4}{x}$,
画函数y=$\frac{4}{x}$和y=x2的图象,
∵关于x的不等式x2+a-$\frac{4}{x}$<0(a>0)只有一个整数解,
∴整数解为x=1,
当x=1时,x2+a-$\frac{4}{x}$=0,
a=3,
∴0<a<3,
故答案为:0<a<3.
点评 本题考查了反比例函数与一次函数的交点问题,利用数形结合的思想是本题的关键,也考查了观察函数图象的能力.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
8.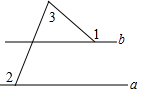 如图,已知直线a∥b,则∠1+∠2-∠3=( )
如图,已知直线a∥b,则∠1+∠2-∠3=( )
 如图,已知直线a∥b,则∠1+∠2-∠3=( )
如图,已知直线a∥b,则∠1+∠2-∠3=( )| A. | 180° | B. | 150° | C. | 135° | D. | 90° |
5.九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:
已知该图书的进价为每本30元,设售价为x元.
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价(元/本) | 50 | 55 | 60 | 65 | … |
| 月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
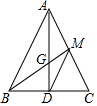 如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.
如图,△ABC中,如果AB=AC,AD⊥BC于点D,M为AC中点,AD与BM交于点G,那么S△GBD:S△MDC为$\frac{2}{3}$.